如图，四棱锥 $P-A B C D$ 中，$P A=P D=A D=C D=2$ ，底面 $A B C D$ 是个直角梯形，$A D / / B C$ ，$\angle D A B=90^{\circ}, \angle A D C=60^{\circ}$ ．

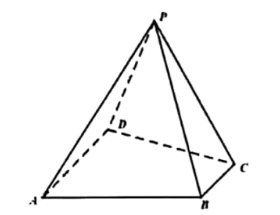
（1）证明：$P C \perp A D$ ；
（2）若二面角 $P-A D-B$ 的大小为 $60^{\circ}$ ，在棱 $P B$ 上是否存在点 $G$（不与端点重合），使得直线$C G$ 与平面 $P A D$ 所成的角的正弦值为 $\frac{\sqrt{21}}{7}$ ？若存在，求 $\frac{P G}{P B}$ 的值，若不存在，说明理由．