单选题 (共 9 题 ),每题只有一个选项正确
已知正方体 $A B C D-A_1 B_1 C_1 D_1$ ,则( )
$\text{A.}$ 直线 $B C_1$ 与 $D A_1$ 所成的角为 $90^{\circ}$
$\text{B.}$ 直线 $B C_1$ 与 $C A_1$ 所成的角为 $90^{\circ}$
$\text{C.}$ 直线 $B C_1$ 与平面 $B B_1 D_1 D$ 所成的角为 $45^{\circ}$
$\text{D.}$ 直线 $B C_1$ 与平面 $A B C D$ 所成的角为 $45^{\circ}$
在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中,$P$ 为 $B_1 D_1$ 的中点,则直线 $P B$ 与 $A D_1$ 所成的角为()
$\text{A.}$ $\frac{\pi}{2}$
$\text{B.}$ $\frac{\pi}{3}$
$\text{C.}$ $\frac{\pi}{4}$
$\text{D.}$ $\frac{\pi}{6}$
如图,点 $N$ 为正方形 $A B C D$ 的中心,$\triangle E C D$ 为正三角形,平面 $E C D \perp$ 平面 $A B C D, M$ 是线段 $E D$ 的中点,则( )
$\text{A.}$ $B M=E N$ ,且直线 $B M, E N$ 是相交直线
$\text{B.}$ $B M \neq E N$ ,且直线 $B M, E N$ 是相交直线
$\text{C.}$ $B M=E N$ ,且直线 $B M, E N$ 是异面直线
$\text{D.}$ $B M \neq E N$ ,且直线 $B M, E N$ 是异面直线
如图所示,$A B C D-A_1 B_1 C_1 D_1$ 是长方体,$O$ 是 $B_1 D_1$ 的中点,直线 $A_1 C$ 交平面 $A B_1 D_1$ 于点 $M$ ,则下列结论正确是( )
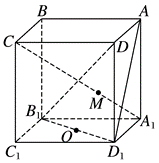
$\text{A.}$ $A, M, O$ 三点共线
$\text{B.}$ $A, M, O, A_1$ 不共面
$\text{C.}$ $A, M, C, O$ 不共面
$\text{D.}$ $B, B_1, O, M$ 共面
在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中,$E$ 为棱 $C C_1$ 的中点,则异面直线 $A E$ 与 $C D$ 所成角的正切值为
$\text{A.}$ $\frac{\sqrt{2}}{2}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ $\frac{\sqrt{5}}{2}$
$\text{D.}$ $\frac{\sqrt{7}}{2}$
如图,在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中,点 $E, F$ 分别在 $A_1 D, A C$ 上,且 $A_1 E=2 E D$ , $C F=2 F A$ ,则 $E F$ 与 $B D_1$ 的位置关系是( )
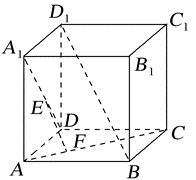
$\text{A.}$ 相交但不垂直
$\text{B.}$ 相交且垂直
$\text{C.}$ 异面
$\text{D.}$ 平行
如图,在底面为正方形,侧棱垂直于底面的四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 中,$A A_1=2 A B=2$ ,则异面直线 $A_1 B$ 与 $A D_1$ 所成角的余弦值为
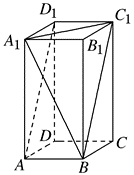
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $\frac{2}{5}$
$\text{C.}$ $\frac{3}{5}$
$\text{D.}$ $\frac{4}{5}$
在长方体 $A B C D-A_1 B_1 C_1 D_1$ 中,$A B=B C=1, A A_1=\sqrt{3}$ ,则异面直线 $A D_1$ 与 $D B_1$ 所成角的余弦值为
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $\frac{\sqrt{5}}{6}$
$\text{C.}$ $\frac{\sqrt{5}}{5}$
$\text{D.}$ $\frac{\sqrt{2}}{2}$
在直三棱柱 $A B C-A_1 B_1 C_1$ 中,底面 $A B C$ 为等腰直角三角形,且斜边 $B C=2, D$ 是 $B C$ 的中点,若 $A A_1=\sqrt{2}$ ,则异面直线 $A_1 C$ 与 $A D$ 所成角的大小为( )
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $45^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $90^{\circ}$
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
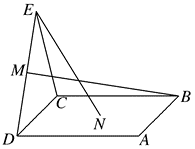
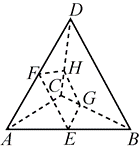
如图,已知空间四边形 $A B C D, E, F$ 分别是 $A B, A D$ 的中点,$G, H$ 分别是 $B C, C D$ 上的点,且 $C G=\frac{1}{3} B C$ , $C H=\frac{1}{3} D C$ .求证:
(1)$E, F, G, H$ 四点共面;
(2)直线 $F H, E G, A C$ 共点.
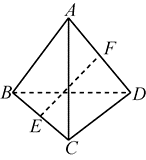
如图,$A$ 是 $\triangle B C D$ 所在平面外的一点,$E, F$ 分别是 $B C, A D$ 的中点.
(1)求证:直线 $E F$ 与 $B D$ 是异面直线;
(2)若 $A C \perp B D, A C=B D$ ,求 $E F$ 与 $B D$ 所成的角的大小.