单选题 (共 5 题 ),每题只有一个选项正确
复数 $z=\frac{5}{2-i}$ 的虚部是
$\text{A.}$ i
$\text{B.}$ $\frac{5}{3}$
$\text{C.}$ $\frac{5}{3} i$
$\text{D.}$ 1
若复数 $z$ 的共轭复数 $\bar{z}$ 满足 $i \cdot \bar{z}=4+3 i$(其中 i 为虚数单位),则 $z \cdot \bar{z}$ 的值为
$\text{A.}$ $\sqrt{7}$
$\text{B.}$ 5
$\text{C.}$ 7
$\text{D.}$ 25
已知向量 $\vec{a}=(2, m), \vec{b}=(4,-1)$ ,且 $(\vec{a}-\vec{b}) \perp(\vec{a}+\vec{b})$ ,则实数 $m=$
$\text{A.}$ 2
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ 8
$\text{D.}$ $\pm \sqrt{13}$
已知 $\vec{a}=(-2,-1), \vec{b}=(1,2)$ ,若向量 $\vec{a}$ 在向量 $\vec{b}$ 上的投影向量为 $\vec{c}$ ,则 $\vec{c}=$
$\text{A.}$ $\left(-\frac{4 \sqrt{5}}{5},-\frac{8 \sqrt{5}}{5}\right)$
$\text{B.}$ $\left(\frac{4 \sqrt{5}}{5},-\frac{8 \sqrt{5}}{5}\right)$
$\text{C.}$ $\left(-\frac{4}{5},-\frac{8}{5}\right)$
$\text{D.}$ $\left(-\frac{8}{5},-\frac{4}{5}\right)$
已知点 $A, B, C$ 均在半径为 $\sqrt{2}$ 的圆上,若 $|A B|=2$ ,则 $\overrightarrow{A C} \cdot \overrightarrow{B C}$ 的最大值为( )
$\text{A.}$ $3+2 \sqrt{2}$
$\text{B.}$ $2+2 \sqrt{2}$
$\text{C.}$ 4
$\text{D.}$ $\sqrt{2}$
多选题 (共 4 题 ),每题有多个选项正确
若复数 $z$ 满足:$z(\bar{z}+2 i)=8+6 i$ ,则( )
$\text{A.}$ $z$ 的实部为 3
$\text{B.}$ $z$ 的虚部为 1
$\text{C.}$ $z \bar{z}=\sqrt{10}$
$\text{D.}$ $z$ 在复平面上对应的点位于第一象限
设 $\vec{a}, \vec{b}, \vec{c}$ 是三个非零向量,且相互不共线,则下列说法正确的是()
$\text{A.}$ 若 $|\vec{a}+\vec{b}|=|\vec{a}-\vec{b}|$ ,则 $\vec{a} \perp \vec{b}$
$\text{B.}$ 若 $|\vec{a}|=|\vec{b}|$ ,则 $(\vec{a}+\vec{b}) \perp(\vec{a}-\vec{b})$
$\text{C.}$ 若 $\vec{a} \cdot \vec{c}=\vec{b} \cdot \vec{c}$ ,则 $\vec{a}-\vec{b}$ 不与 $\vec{c}$ 垂直
$\text{D.}$ $(\vec{b} \cdot \vec{c}) \vec{a}-(\vec{a} \cdot \vec{c}) \vec{b}$ 不与 $\vec{c}$ 垂直
已知平面向量 $\vec{a}=(-2,1), \vec{b}=(4,2), \vec{c}=(2, t)$ ,则下列说法正确的是( )
$\text{A.}$ 若 $\vec{a} / / \vec{c}$ ,则 $t=-1$
$\text{B.}$ 若 $\vec{b} \perp \vec{c}$ ,则 $t=-4$
$\text{C.}$ 若 $t=1$ ,则向量 $\vec{a}$ 在 $\vec{c}$ 上的投影向量为 $\frac{3}{5} \vec{c}$
$\text{D.}$ 若 $t > -4$ ,则向量 $\vec{b}$ 与 $\vec{c}$ 的夹角为锐角
"圆幂定理"是平面几何中关于圆的一个重要定理,它包含三个结论,其中一个是相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.如图,已知圆 $O$ 的半径为 2 ,点 $P$ 是圆 $O$ 内的定点,且 $ A C, B D$ 均过点 $P$ ,则下列说法正确的是( )
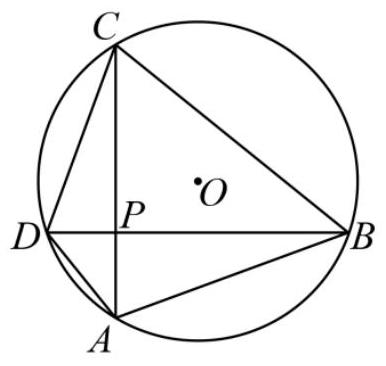
$\text{A.}$ $\overrightarrow{P A} \cdot \overrightarrow{P C}$ 为定值
$\text{B.}$ $\overrightarrow{O A} \cdot \overrightarrow{O C}$ 的取值范围是 $[-2,0]$
$\text{C.}$ 当 $A C \perp B D$ 时, $\overrightarrow{A B} \cdot \overrightarrow{C D}$ 为定值
$\text{D.}$ $A C \perp B D$ 时,$|\overrightarrow{A C}| \cdot|\overrightarrow{B D}|$ 的最大值为 12
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知平面向量 $\stackrel{1}{a}=(-2,4), \quad \vec{b}=(\lambda, 1)$ ,若 $\vec{a}$ 与 $\vec{b}$ 垂直,则实数 $\lambda=$ $\qquad$ .
复数 $z=\frac{1+i}{2-i}$ 的虚部是 $\qquad$ .
已知点 $D$ 为 $\triangle A B C$ 的边 $B C$ 的中点, $\overrightarrow{A B}=\vec{a}+\vec{b}, \overrightarrow{A C}=\vec{a}-2 \vec{b},|\vec{a}|=2|\vec{b}|=2, \vec{a}, \vec{b}$ 的夹角为 $\frac{\pi}{3}$ ,则 $|\overrightarrow{A D}|=$ $\qquad$。
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知向量 $\vec{a}=(2,3),|\vec{b}|=2 \sqrt{13}$ .
(1)若 $\vec{a} / / \vec{b}$ ,求 $\vec{b}$ 的坐标;
(2)若 $(5 \vec{a}-2 \vec{b}) \perp(\vec{a}+\vec{b})$ ,求 $\vec{a}$ 与 $\vec{b}$ 的夹角.
计算下列各题:
(1)$\frac{(1+i)^{5}}{1-i}+\frac{(1-i)^{5}}{1+i}$ ;
(2)$\left(\frac{1+i}{1-i}\right)^{2019}-\left(\frac{1-i}{1+i}\right)^{2019}$ ;
计算
(3)$\left|\frac{(4-3 i)^{5}(1-\sqrt{3} i)^{4}}{(4+2 i)^{8}}\right|$ ;
(4)$i+2 i^{2}+3 i^{3}+\cdots+2019 i^{2019}+2020 i^{2020}$ .
已知 $\vec{a}=(2 \sin x, 1), \vec{b}=(\cos x-\sin x, 1)$ ,函数 $f(x)=\stackrel{\rightharpoonup}{a} \cdot \stackrel{\rightharpoonup}{b}$ .
(1)求 $f(x)$ 的最小正周期;
(2)求 $f(x)$ 的单调减区间;
(3)求 $f(x)$ 在区间 $\left[-\frac{\pi}{8}, \frac{3 \pi}{8}\right]$ 上的最大值.
已知点 $D, P$ 在锐角 $\triangle A B C$ 所在的平面内,且满足 $\overrightarrow{A D}=2 \overrightarrow{D C}, \overrightarrow{B P}=3 \overrightarrow{B D}$ .
(1)若 $\overrightarrow{A P}=x \overrightarrow{A B}+y \overrightarrow{A C}$ ,求实数 $x, y$ 的值;
(2)已知 $\overrightarrow{A P} \cdot \overrightarrow{B C}=4 S$ ,其中 $S$ 为 $\triangle A B C$ 的面积.
① 求证: $\tan B+\tan C=\tan B \tan C$ ;
② 求 $\tan B \tan C$ 的最小值,并求此时 $\tan A$ 的值.
在等腰梯形 $A B C D$ 中,已知 $A B / / D C, A B=4, B C=2, \angle A B C=60^{\circ}$ ,动点 $E$ 和 $F$ 分别在线段 $B C$ 和 $D C$ 上 (含端点),且 $\overrightarrow{B E}=m \overrightarrow{B C}, \overrightarrow{D F}=n \overrightarrow{D C}$ 且( $m 、 n$ 为常数),设 $\overrightarrow{A B}=\vec{a}, \overrightarrow{B C}=\vec{b}$ .

(I)试用 $\vec{a} 、 \vec{b}$ 表示 $\overrightarrow{A E}$ 和 $\overrightarrow{A F}$ ;
(II)若 $m+n=1$ ,求 $\overrightarrow{A E} \cdot \overrightarrow{A F}$ 的最小值.
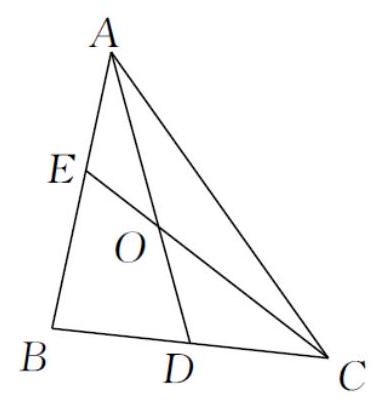
在 $\triangle A B C$ 中,已知 $A B=2, A C=\sqrt{11}, \cos \angle B A C=\frac{5 \sqrt{11}}{22}, D$ 为 $B C$ 的中点,$E$为 $A B$ 边上的一个动点,$A D$ 与 $C E$ 交于点 $O$ .设 $\overrightarrow{A E}=x \overrightarrow{A B}$ .
(1)若 $x=\frac{1}{4}$ ,求 $\frac{C O}{O E}$ 的值;
(2)求 $\overrightarrow{A O} \cdot \overrightarrow{C E}$ 的最小值.