单选题 (共 2 题 ),每题只有一个选项正确
已知 $m, n \in R$ ,且 $m-3 n+4=0$ ,则 $2^m+\frac{1}{8^n}$ 的最小值为()
$\text{A.}$ $\frac{257}{64}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{\sqrt{2}}{2}$
$\text{D.}$ $\frac{1}{2}$
已知 $a>0, b>0,3 a+\frac{4}{b}=1$ ,则 $\frac{1}{a}+3 b$ 的最小值为
$\text{A.}$ 13
$\text{B.}$ 19
$\text{C.}$ 21
$\text{D.}$ 27
多选题 (共 6 题 ),每题有多个选项正确
已知实数 $a, b$ 满足 $\ln a+\ln b=\ln (a+4 b)$ ,则下列结论正确的是( )
$\text{A.}$ $a b$ 的最小值为 16
$\text{B.}$ $a+b$ 的最大值为 9
$\text{C.}$ $a b$ 的最大值为 9
$\text{D.}$ $\sqrt{\frac{4}{a}}+\sqrt{\frac{1}{b}}$ 的最大值为 $\sqrt{2}$
下面描述正确的是( )
$\text{A.}$ 已知 $a>0, b>0$ ,且 $a+b=1$ ,则 $\log _2 a+\log _2 b \leq-2$
$\text{B.}$ 函数 $f(x)=|\lg x|$ ,若 $0 < a < b$ ,且 $f(a)=f(b)$ ,则 $a +2 b$ 的最小值是 $2 \sqrt{2}$
$\text{C.}$ 已知 $\frac{1}{x+1}+\frac{2}{2 x+y}=1(x>0, y>0)$ ,则 $3 x+y$ 的最小值为 $2+2 \sqrt{2}$
$\text{D.}$ 已知 $x^2+y^2-x-y-x y+2=0(x>0, y>0)$ ,则 $x y$ 的最小值为 $\frac{7}{12}$
已知正数 $a, b$ 满足 $a+2 b=2 a b$ ,则下列说法一定正确的是( )
$\text{A.}$ $a+2 b \geq 4$
$\text{B.}$ $a+b \geq 4$
$\text{C.}$ $a b \geq 8$
$\text{D.}$ $a^2+4 b^2 \geq 8$
已知 $x^2+y^2=4(x y \neq 0)$ ,则下列结论正确的是( )
$\text{A.}$ $|x+y| \leq 2 \sqrt{2}$
$\text{B.}$ $|x y| \leq 2$
$\text{C.}$ $\log _2|x|+\log _2|y| < \sqrt{2}$
$\text{D.}$ $\frac{1}{|x|}+\frac{1}{|y|}>\sqrt{2}$
若 $a>0, b>0$ ,且 $a+b=4$ ,则下列不等式恒成立的是()
$\text{A.}$ $0 < \frac{1}{a b} \leq \frac{1}{4}$
$\text{B.}$ $\frac{1}{a}+\frac{1}{b} \geq 1$
$\text{C.}$ $\log _2 a+\log _2 b < 2$
$\text{D.}$ $\frac{1}{a^2+b^2} \leq \frac{1}{8}$
已知实数 $a>0, b>0, a+b=1$ .则下列不等式正确的是( )
$\text{A.}$ $2^a+2^b \geq 2 \sqrt{2}$
$\text{B.}$ $\sqrt{a}+\sqrt{b} \leq \sqrt{2}$
$\text{C.}$ $\left(\frac{1}{a}+2\right)\left(\frac{1}{b}+2\right) \leq 16$
$\text{D.}$ $\frac{2 a}{a^2+b}+\frac{b}{b^2+a} \leq \frac{3+2 \sqrt{3}}{3}$
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
工厂某种产品的年固定成本为 250 万元,每生产 $x$ 千件,另需投入成本 $C(x)$(单位:万元),当年产量不足 80 千件时,$C(x)=\frac{1}{3} x^2+10 x$ ;当年产量不小于 80 千件时,$C(x)=51 x+\frac{10000}{x}-$ 1450 .已知每件商品的售价为 0.05 万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 $L(x)$(万元)关于年产量 $x$(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
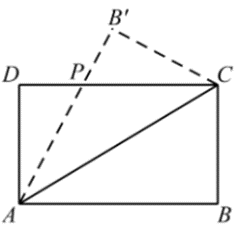
设矩形 $A B C D(A B>B C)$ 的周长为 $12+6 \sqrt{2}$ ,把它沿对角线 $A C$ 对折后,设 $A B$ 交 $D C$ 于点 $P$ ,此时点 $B$ 记作 $B^{\prime}$ ,如图所示,设 $A D=x, D P=y$ ,则 $\triangle A D P$ 的面积的最大值为