解答题 (共 14 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $F(x)$ 是分布函数,证明:对于任意 $h>0$ ,函数
$$
G(x)=\frac{1}{2 h} \int_{x-h}^{x+h} F(t) d t
$$
也是某一随机变量的分布函数。
试确定 $A$ 的值,使
$$
p_i=\frac{A}{i(i+1)} \quad i=1,2, \cdots
$$
能成为离散型随机变量的概率分布.
一批产品中有 10 件正品, 3 件次品.现从中随机地一件一件取出,以 $X$ 表示直到取得正品为止所需的次数,分别求出在下列各种情形下,$X$ 的概率分布。
(1)每次取出的产品不放回;
(2)每次取出的产品经检验后放回,再抽取;
(3)每次取出一件产品后,总以一件正品放回,再抽取.
已知随机变量 $X$ 的分布函数为
$$
F(x)= \begin{cases}0 & x < -1 \\ 0.3 & -1 \leqslant x < 0 \\ 0.6 & 0 \leqslant x < 1 \\ 0.8 & 1 \leqslant x < 3 \\ 1 & x \geqslant 3\end{cases}
$$
试求 $X$ 的概率分布,并计算 $P(X < 1 \mid X \neq 0)$ .
某一专业射击手独立地射击 5 次,若击中目标一次和二次的概率相等,求其击中目标 4 次的概率。
假设昆虫产卵个数 $X$ 服从普阿松分布 $P(\lambda)$ ,而每个卵孵化成幼虫的概率为 $p$ ,并各个卵是否瓜化为幼虫是相互独立的.试求一只昆虫所生的幼虫数 $Y$ 的概率分布。
有 10 个乒乓球,其中 5 个新的, 5 个旧的.任取 1 个比赛使用,用完后放回。第二次再从中取出 2 个,令 $X$ 表示取出的 2 个中的新球个数。求 $X$ 的概率分布和分布函数。
设随机变量 $X$ 的分布函数为
$$
F(x)= \begin{cases}1-(1+x) e^{-x} & x \geqslant 0 \\ 0 & x < 0\end{cases}
$$
试求:(1)$X$ 的密度函数;
(2)$P(X < 1), P(X \geqslant 2)$ 和 $P(1 \leqslant X < 2)$ .
设随机变量 $X$ 的绝对值不大于 $1, P(X=-1)=\frac{1}{8}$ , $P(X=1)=\frac{1}{4}$ .在事件 $\{-1 < X < 1\}$ 出现的条件下,$X$ 在 $(-1,1)$ 内的任一子区间上取值的条件概率与该子区间长度成正比,试求 $X$ 的分布函数。
设连续型随机变量X的分布函数为
$$
F(x)= \begin{cases}a & x < 1 \\ b x \ln x+c x+d & 1 \leqslant x < e \\ d & x \geqslant e\end{cases}
$$
试确定常数 $a, b, c, d$ 的值,并求 $X$ 的密度函数.
设随机变量 $X \sim U[0,5]$ ,现在对 $X$ 进行三次独立观测,试求至少有两次观测值使方程 $4 x^2+4 X x+(X+2)=0$ 有实根的概率.
在电源电压不超过 200 伏,在 $200 \sim 240$ 伏和超过 240 伏 3 种情况下,某种电子元件损坏的概率分别为 $0.1, ~ 0.001$ 和 0.2 ,假定电源电压 $X \sim N\left(220,25^2\right)$ ,试求:(1)电子元件损坏的概率 $\alpha$ ;(2)在电子元件损坏时,电源电压在 $200 \sim 240$ 伏的概率 $\beta$ .
设随机变量X的分布列为
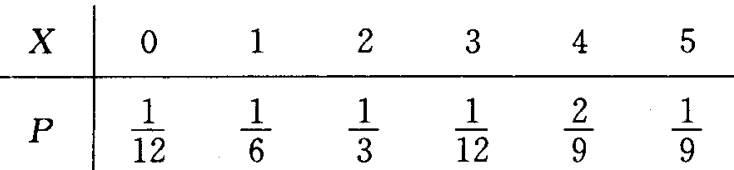
试求:(1)$Y=2 X+1$ 的分布列;
(2)$Y=(X-2)^2$ 的分布列.
设随机变量 $X$ 的密度函数为 $p_X(x)=\frac{1}{\pi\left(1+x^2\right)}$ ,试求 $Y$ $=1-\sqrt[3]{X}$ 的密度函数 $p_Y(y)$ .