解答题 (共 26 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
一批零件中有九个合格品与三个废品.安装机器时从这批零件中任取一个,如果取出时是废品就不再放回,求在取得合格品以前已取出废品数的数学期望和方差。
设随机变量 $X$ 的密度函数为
$$
p(x)=\frac{1}{2 a} e^{-\frac{|x-b|}{a}}
$$
其中 $a>0$ ,求数学期望 $E X$ 和方差 $D X$ .
求掷 $n$ 颗骰子出现点数之和的数学期望与方差.
二维随机向量 $(X, Y)$ 的联合概率分布为
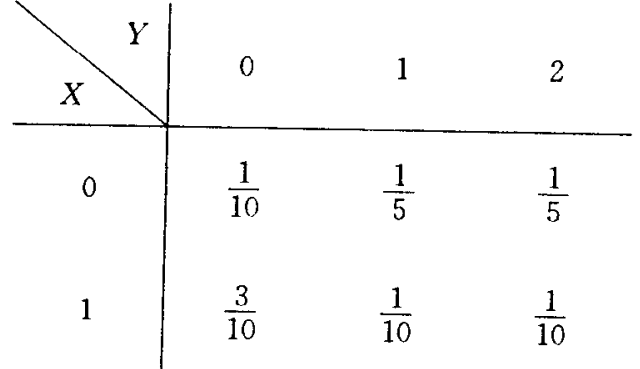
求 $\rho_{X Y}$ 和 $D(X-Y)$ .
已知二维随机向量 $(X, Y)$ 的联合密度函数为
$$
p(x, y)= \begin{cases}8 x y & 0 \leqslant y \leqslant x, 0 \leqslant x \leqslant 1 \\ 0 & \text { 其他 }\end{cases}
$$
试求 $\rho_{X X^{\prime}}$ 和 $D(5 X-3 Y+4)$ .
将 $n$ 封不同的信的 $n$ 张信䇝与 $n$ 个信封进行随机匹配,求匹配成对数的数学期望与方差。
假设昆虫产卵个数 $X$ 服从普阿松分布 $P(\lambda)$ ,而每个卵孵化成幼虫的概率为 $p$ ,并且各个卵是否粰化为幼虫是相互独立的.试求一只昆虫所生的幼虫数 $Y$ 的概率分布,数学期望和方差。
已知二维随机向量 $(X, Y)$ 的联合密度函数为
$$
p(x, y)=A e^{-\left[(x+5)^2+8(x+5)(y-3)+25(y-3)^2\right]}
$$
求:(1)系数 $A$ ;
(2)$E X, E Y, D X$ 和 $D Y$ ;
(3)$\rho_{X Y}$ ;
(4)$X$ 和 $Y$ 的分布.
设随机变量 $X$ 的密度函数为
$$
p(x)=\left\{\begin{array}{cc}
\frac{2}{\pi} \cos ^2 x & |x| \leqslant \frac{\pi}{2} \\
0 & |x|>\frac{\pi}{2}
\end{array}\right.
$$
求 $E(\sin X)$ 和 $D(\sin X)$ .
设随机变量 $X$ 和 $Y$ 相互独立,且同服从正态分布 $N\left(\mu, \sigma^2\right)$ ,求 $E[\max \{X, Y\}]$ 。
有 5 个相互独立工作的电子装置,它们的寿命 $X_k(k=1$ , $2,3,4,5$ )服从同一个平均寿命为 $\frac{1}{\lambda}$ 的指数分布。
(1)若将这 5 个电子装置串联组成整机,其中有一个装置损坏,则整机就不能工作,求整机寿命 $Y$ 的数学期望;
(2)若将这 5 个电子装置并联组成整机,全部装置损坏时,整机才不能工作,求整机寿命 $Z$ 的数学期望。
设某种产品每周需求量 $Q$ 取 $1,2, \cdots, 9$ 为其值是等可能的,生产每件产品成本是 $c_1=3$ 元,每件产品售价为 $c_2=9$ 元;没有售出的产品以 $c_3=1$ 元的费用存人仓库,问生产者每周生产多少件产品能使所获利润的期望最大?
报童问题)报童每天从邮局订购零售报纸,批发价为 0.4元/份,而每天报纸的需求量 $X$ 是服从 $N(150,36)$ 的随机变量,零售价为 0.6 元/份,如果当天的报纸卖不掉,他就按每份 0.2 元处理掉。为使获利最大,报童每天应向邮局订购多少份报纸?
假设有 10 只同种电器元件,其中有 2 只废品.装配仪器时,从这批元件中任取一只,如是废品则扔掉,重新任取一只,如仍是废品则扔掉,再取一只,试求在取到正品之前,已取出的废品只数的数学期望和方差.
从一个装有 $m$ 个白球和 $n$ 个黑球的袋中取球,直到出现白球时为止,如果每次取出的球仍放回袋中,求取出黑球数的数学期望与方差。
从学校乘汽车到火车站,途中有 3 个交通岗,假设在各交通岗遇到红灯的事件是相互独立的,并且概率都是 0.4 ,设 $X$ 为途中遇到的红灯的次数,求 $X$ 的概率分布,"平均停的次数"和 $D X$ .
已知甲,乙两箱中装有同种产品,其中甲箱中装有 3 件合格品和 3 件次品,乙箱中仅装有 3 件合格品.从甲箱中任取 3 件产品放人乙箱后,求:
(1)乙箱中次品件数的数学期望;
(2)从乙箱中任取一件产品是次品的概率.
设随机变量 $X$ 的分布函数为
$$
F(x)=\left\{\begin{array}{cc}
1-\frac{a^3}{x^3} & x \geqslant a \\
0 & x < a
\end{array}\right.
$$
其中 $a>0$ 为常数,求 $E X$ 和 $D X$ .
设随机变量 $X$ 的密度函数为
$$
p(x)=\left\{\begin{array}{cc}
\frac{b}{a}(a-|x|) & |x| \leqslant a \\
0 & \text { 其他 }
\end{array}\right.
$$
且已知方差 $D X=1$ ,求常数 $a$ 和 $b$ .
假设一厂家生产的每台仪器以概率 0.70 可以直接出厂,以概率 0.30 需进一步调试,经调试后以概率 0.80 可以出厂,以概率 0.20定为不合格品不能出厂。现该厂新生产了 20 台仪器(假设各台仪器的生产过程相互独立)。求:
(1)一台仪器能出厂的概率 $p$ ;
(2)其中恰好有两件不能出厂的概率 $\alpha$ ;
(3)其中至少有两件不能出厂的概率 $\beta$ ;
(4)平均能出厂的台数.
设有 10 台同种设备同时开始作独立的寿命试验.若此种设备寿命服从期望寿命为 800 天的指数分布。求试验开始后 400 天内发现有 3 台设备失效的概率.
设随机变量 $X$ 的密度函数为
$$
p(x)=\left\{\begin{array}{cc}
\frac{1}{\pi \sqrt{1-x^2}} & |x| < 1 \\
0 & |x| \geqslant 1
\end{array}\right.
$$
求 $D X$ .
箱中装有 $n$ 只球,其中白球数为随机变量 $X$ ,已知 $E X=n$ ,试求从箱中任取一球为白球的概率。
设 $E X^2$ 存在,$c$ 为任意常数,问 $c$ 为何值时 $E(X-c)^2$ 取最小值?
设 $X$ 为连续型随机变量,其密度函数为 $p(x)$ ,且当 $x \in[a, b]$时,$p(x) \neq 0$ ;当 $x \notin[a, b]$ 时,$p(x)=0$ ,求证:
$a \leqslant E X \leqslant b, D X \leqslant\left(\frac{b-a}{2}\right)^2$.
设随机变量 $X$ 和 $Y$ 相互独立,证明 $D(X Y \geqslant D X \cdot D Y$ .