一、单选题 (共 2 题 ),每题只有一个选项正确
1. 已知二维随机变量 的分布函数为 , 则
2. 设随机变量
相互独立, 且根率分布分别为
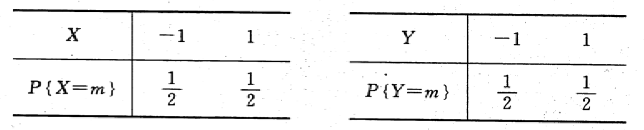
则下列式子中正确的是()。
二、填空题 (共 3 题 ),请把答案直接填写在答题纸上
3. 已知二维随机变量
的分布律为
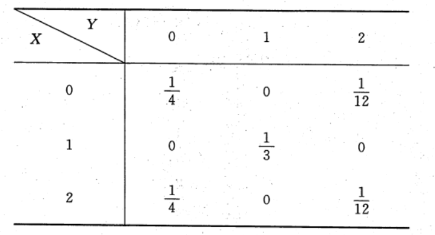
则
4. 设随机变量
与
有相同的概率分布
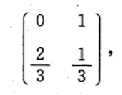
并且满足
, 则
的分布律为
5. 已知二维随机变量 在矩形区域 上服从均匀分布, 则
三、解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
6. 设二维随机变量 的概率密度为
其他
求: (1) ;
(2) .
7. 已知随机变量 与 的概率分布分别为
且 .
(1) 求 与 的联合分布律;
(2) 问 与 是否独立? 为什么?
8. 设二维连续型随机变量 的概率密度为
其他
求随机变量 的概率密度.
9. 设随机变量 和 的联合分布是正方形 上的均匀分布,求随机变量 的概率密度 .
10. 已知随机变量
相互独立,
服从标准正态分布,
的概率分布为
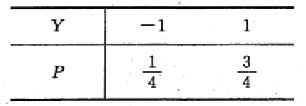
求
的概率密度
.