单选题 (共 6 题 ),每题只有一个选项正确
设 $A, B, C$ 足三个随机变量, 则事件 “ $A, B, C$ 不多于一个发生” 的逆事件为
$\text{A.}$ $A, B, C$ 都发生
$\text{B.}$ $A, B, C$ 至少有一个发生
$\text{C.}$ $A, B, C$ 都不发生
$\text{D.}$ $A, B, C$ 至少有两个发生
设随机变量 $X$ 的概率密度为 $f(x)$, 且满足 $f(x)=f(-x), F(x)$ 为 $X$ 的分布函数, 则 对任意实数 $a$, 下列式子中成立的是
$\text{A.}$ $F(-a)=\frac{1}{2}-\int_0^a f(x) \mathrm{d} x$
$\text{B.}$ $F(-a)=1-\int_0^a f(x) \mathrm{d} x$
$\text{C.}$ $F(a)=F(-a)$
$\text{D.}$ $F(-a)=2 F(a)-1$
设随机变量 $X, Y$ 相互独立, $\boldsymbol{F}_{\boldsymbol{X}}(\boldsymbol{x})$ 与 $\boldsymbol{F}_{\boldsymbol{Y}}(\boldsymbol{y})$ 分别是 $X$ 与 $Y$ 的分布函数, 则随机 变量 $Z=\max \{X, Y\}$ 分布函数 $\boldsymbol{F}_{\mathbf{Z}}(\mathbf{z})$ 为
$\text{A.}$ $\max \left\{F_X(z), F_Y(z)\right\}$
$\text{B.}$ $F_X(z)+F_Y(z)-F_X(z) F_Y(z)$
$\text{C.}$ $F_X(z) F_Y(z)$
$\text{D.}$ $F_X(z)$ 或 $F_Y({z})$
设两个相互独立的随机变量 $X$ 和 $Y$ 分别服从正态分布 $N(0,1)$ 和 $N(1,1)$, 则
$\text{A.}$ $P\{X+Y \leq 0\}=\frac{1}{2}$
$\text{B.}$ $P\{X+Y \leq 1\}=\frac{1}{2}$
$\text{C.}$ $P\{X-Y \leq 0\}=\frac{1}{2}$
$\text{D.}$ $P\{X-Y \leq 1\}=\frac{1}{2}$
对任意两个随机变量 $X$ 和 $Y$, 若 $E(X Y)=E(X) E(Y)$, 则
$\text{A.}$ $X$ 和 $Y$ 独立
$\text{B.}$ $X$ 和 $Y$ 不独立
$\text{C.}$ $D(X Y)=D(X) D(Y)$
$\text{D.}$ $D(X+Y)=D(X)+D(Y)$
设 $X_1, X_2, \ldots, X_n(n \geq 3)$ 为来自总体 $X$ 的一个简单随机样本, 则下列估计量中不是总体期望 $\mu$ 的无偏估计量的是
$\text{A.}$ $\bar{X}$
$\text{B.}$ $0.1 \times\left(6 X_1+4 X_2\right)$
$\text{C.}$ $X_1+X_2+\cdots+X_n$
$\text{D.}$ $X_1+X_2-X_3$
填空题 (共 8 题 ),请把答案直接填写在答题纸上
设 $A 、 B$ 为随机事件, $P(A)=0.3, P(B)=0.4$, 若 $P(A \mid B)=0.5$, 则 $P(A \cup B)=$ ________
若 $A$ 与 $B$ 相互独立, 则 $P(A \cup B)=$ ________
设随机变量 $X$ 在区间 $[1,6]$ 上服从均匀分布,则 $P\{1 < X < 3\}=$
设随机变量 $X$ 的分布函数为 $F(x)=\left\{\begin{array}{cc}0, & x < -1 \\ 0.3, & -1 \leq x < 1 \\ 0.6, & 1 \leq x < 2 \\ 1, & x \geq 2\end{array}\right.$, 则 $X$ 的分布律为
若离散型随机变量 $X$ 的分布律为
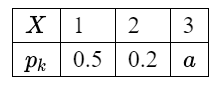
则常数 $a=$ ; 又 $Y=2 X+3$, 则 $P\{Y>5\}=$
设随机变量 $X$ 服从二项分布 $b(50,0.2)$, 则 $E(X)=$ , $D(X)=$
设随机变量 $X \sim N(0,1), Y \sim N(1,3)$, 且 $X$ 和 $Y$ 相互独立, 则 $D(3 X-2 Y)=$
设随机变量 $X$ 的数学期望 $E(X)=\mu$, 方差 $D(X)=\sigma^2$, 则由切比雪夫不等式有 $P\{\mid X$ $-\mu \mid < 3 \sigma\} \geq$
从正态总体 $N\left(\mu, 0.1^2\right)$ 随机抽取的容量为 16 的简单随机样本, 测得样本均值 $\overline{\boldsymbol{x}}=\mathbf{5}$, 则末知参数 $\mu$ 的置信度为 0.95 的置信区间是 (用抽样分布的上侧分位点表示).
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某大型连锁超市采购的某批商品中, 申、乙、丙三厂生产的产品 分别占 $45 \% 、 35 \% 、 20 \%$, 各厂商的次品率分别为 $4 \% 、 2 \% 、 5 \%$, 现从中任取一件产品, (1) 求这件产品是次品的概率; (2) 若这件产品是次品, 求它是甲厂生产的概率?
设连续型随机变量 $X$ 的概率密度为 $f(x)=\left\{\begin{array}{cc}A \sin x, 0 < x < \pi \\ 0, & \text { 其他 }\end{array}\right.$,
求: (1) 常数 $A$ 的值;
(2) 随机变量 $X$ 的分布函数 $F(x)$;
(3) $P\left\{\frac{\pi}{3} \leq X \leq \frac{\pi}{2}\right\}$.
设二维随机变量 $(X, Y)$ 的联合概率密度为
$$
f(x, y)=\left\{\begin{array}{cc}
(2-x) y, & 0 \leq x \leq 2,0 \leq y \leq 1 \\
0, & \text { 其他 }
\end{array}\right.
$$
求: (1) 求 $X, Y$ 的边缘概率密度 $f_X(x), f_Y(y)$, 并判断 $X$ 与 $Y$ 是否相互独立(说明原因)?
(2) 求 $P\{X+Y \leq 1\}$.
已知随机变量 $X$ 分布律为
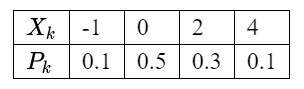
求 $E(X), D(X)$.
设某供电区域中共有 10000 盏电灯, 夜晩每盏灯开着的概率均为 0.7 , 假设各灯开、关时间彼此独立, 求夜晩同时开着的灯的数量在 6800 至 7200 间的概 率.(其中 $\left.\Phi\left(\frac{20}{\sqrt{21}}\right) \approx \Phi(4.36)=0.999999\right)$.
设总体$X$的概率密度为
$
f(x)=\left\{\begin{array}{cc}
(\theta+1) x^\theta, & 0 < x < 1 \\
0, & \text { 其他 }
\end{array}\right.
$
其中$\theta>-1$ 是末知参数, $X_1, X_2, \ldots, X_n$ 为来白总体的一个简单随机样本, $x_1, x_2, \ldots, x_n$ 为样本值, 求 $\theta$ 的矩 估计量和极大似然估计量.