单选题 (共 8 题 ),每题只有一个选项正确
已知复数 $z$ 满足 $\frac{z(1+\mathrm{i})}{2+\mathrm{i}}=1$ ,则 $|z|=$
$\text{A.}$ $\frac{\sqrt{10}}{2}$
$\text{B.}$ $\sqrt{10}$
$\text{C.}$ $\sqrt{5}$
$\text{D.}$ 5
已知集合 $A=\{x \in \mathbf{N} \mid-1 < x < 4\}, B=\left\{y \mid y=x^2, x \in A\right\}$ ,则 $A \cap B=$
$\text{A.}$ $[0,4)$
$\text{B.}$ $(1,4)$
$\text{C.}$ $\{0,1\}$
$\text{D.}$ $\{1\}$
已知数列 $\left\{a_n\right\}$ 为等比数列,$a_1 a_4 a_7=64, a_6 a_7=8$ ,则 $a_9=$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 4
$\text{D.}$ 6
已知函数 $f(x)=-x^2+3 x$ ,则函数 $f(x)$ 在点 $(1, f(1))$ 处的切线方程为
$\text{A.}$ $x+y-3=0$
$\text{B.}$ $x-y+1=0$
$\text{C.}$ $x+y-2=0$
$\text{D.}$ $x-y-1=0$
在 $\triangle A B C$ 中,若 $\overrightarrow{B D}=\mu \overrightarrow{B C}, \overrightarrow{A D}=\frac{2}{5} \overrightarrow{A C}+\lambda \overrightarrow{A B}$ ,则 $\lambda+\mu=$
$\text{A.}$ $\frac{4}{5}$
$\text{B.}$ $\frac{6}{5}$
$\text{C.}$ 1
$\text{D.}$ $\frac{19}{15}$
已知 $\frac{1-\cos 2 \alpha}{\sin 2 \alpha}=2$ ,则 $\sin \alpha(\sin \alpha+\cos \alpha)=$
$\text{A.}$ 2
$\text{B.}$ $\frac{10}{3}$
$\text{C.}$ $\frac{8}{5}$
$\text{D.}$ $\frac{6}{5}$
已知函数 $f(x)=\left|2^x-2\right|$ ,若 $x_1 < x_2$ 且 $f\left(x_1\right)=f\left(x_2\right)$ ,则 $2^{-x_1}+2^{2-x_2}$ 的最小值为
$\text{A.}$ $\frac{9}{4}$
$\text{B.}$ 9
$\text{C.}$ $5+2 \sqrt{2}$
$\text{D.}$ $\frac{3+2 \sqrt{2}}{4}$
已知函数 $f(x)=2 \sin (\omega x+\varphi)(\omega>0)$ 在区间 $\left(\frac{\pi}{6}, \frac{2 \pi}{3}\right)$ 上单调,且满足 $f\left(-\frac{\pi}{6}\right)=f\left(\frac{\pi}{2}\right)$ ,若函数 $f(x)$ 在 $\left(\frac{\pi}{6}, 2 \pi\right)$ 上有且仅有 3 个极值点,则 $\omega$ 的取值范围为
$\text{A.}$ $\left[\frac{18}{11}, \frac{24}{11}\right)$
$\text{B.}$ $\left(\frac{18}{11}, \frac{24}{11}\right]$
$\text{C.}$ $\left[\frac{18}{11}, 2\right)$
$\text{D.}$ $\left(\frac{18}{11}, 2\right]$
多选题 (共 3 题 ),每题有多个选项正确
为了得到函数 $y=\log _2(2 x)$ 的图象,只需将函数 $y=\log _{\sqrt{2}}(\sqrt{x})$ 的图象上所有点
$\text{A.}$ 横坐标变成原来的 $\frac{1}{2}$(纵坐标不变)
$\text{B.}$ 横坐标变成原来的 2 倍(纵坐标不变)
$\text{C.}$ 向上平移 1 个单位长度
$\text{D.}$ 向左平移 1 个单位长度
设等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$ ,公差为 $d$ ,首项为 $a_1$ ,若 $S_8>S_2, S_{11} < 0$ ,则下列结论正确的是
$\text{A.}$ $d < 0$
$\text{B.}$ 当 $n=5$ 时,$S_n$ 取最大值
$\text{C.}$ $\left|a_5\right| < \left|a_6\right|$
$\text{D.}$ 数列 $\left\{\frac{S_n}{n}\right\}$ 为等差数列并且与数列 $\left\{a_n\right\}$ 具有相同的单调性
在棱长为 2 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $\overrightarrow{A P}=x \overrightarrow{A B}+y \overrightarrow{A D}+z \overrightarrow{A A_1}$ ,则
$\text{A.}$ 若 $x+y+z=1$ ,则 $A C_1 \perp B P$
$\text{B.}$ 若 $z=1, x+y=1$ ,且 $x \geqslant 0, y \geqslant 0$ ,则直线 $A P$ 与 $B D$ 所成角的最小角为 $\frac{\pi}{6}$
$\text{C.}$ 若 $x+y+z=\frac{1}{2}$ ,则点 $P$ 所在的平面截正方体所得的截面面积为 $\frac{\sqrt{3}}{2}$
$\text{D.}$ 若 $x+y+z=2$ ,则直线 $C C_1$ 和直线 $D_1 P$ 所成角可能为 $\frac{\pi}{6}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
函数 $f(x)=\tan \left(x+\frac{\pi}{4}\right)$ 的定义域为
两个非零向量 $\boldsymbol{a}, \boldsymbol{b}$ ,满足 $|\boldsymbol{a}+\boldsymbol{b}|=2|\boldsymbol{a}-\boldsymbol{b}|$ ,则向量 $\boldsymbol{a}$ 与向量 $\boldsymbol{b}$ 夹角的余弦值的最小值为
已知函数 $f(x)=\ln \left(\sqrt{x^2-2 x+2}+x-1\right)$ ,数列 $\left\{a_n\right\}$ 为公差不为 0 的等差数列,若 $f\left(a_1\right) +f\left(a_2\right)+f\left(a_3\right)+f\left(a_4\right)+f\left(a_5\right)=0$ ,则 $a_1+a_2+a_3+a_4+a_5=$
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left\{a_n\right\}$ 满足 $a_1=2$ ,且 $\frac{a_{n+1}}{a_n}=\frac{2(2 n+1)}{2 n-1}$ .
(1)求数列 $\left\{a_n\right\}$ 的通项公式;
(2)求数列 $\left\{a_n\right\}$ 的前 $n$ 项和 $S_n$ .
已知函数 $f(x)=\sin \left(2 x+\frac{\pi}{6}\right) \cos \varphi+\cos \left(2 x+\frac{\pi}{6}\right) \sin \varphi(0 < \varphi < \pi)$ 的图象关于点 $\left(\frac{\pi}{3}, 0\right)$ 对称.
(1)求 $\varphi$ ;
(2)若 $x \in\left[0, \frac{\pi}{2}\right]$ ,求函数 $f(x)$ 的最值及取最值时的 $x$ 的值;
(3)若 $0 < \alpha < \pi$ ,且 $f\left(\frac{\alpha}{2}\right)=\frac{1}{4}$ ,求 $\cos (\alpha+\varphi)$ 。
在 $\triangle A B C$ 中,角 $A, B, C$ 的对边分别为 $a, b, c$ ,且 $a \sin C=2 \sqrt{2} c \cos B \cos C-2 \sqrt{2} b \sin ^2 C$ , $a \sin B=4 \sqrt{2}$ .
(1)求 $b$ ;
(2)若 $B C$ 边上的高为 $\frac{20 \sqrt{2}}{9}$ ,求 $\triangle A B C$ 的周长.
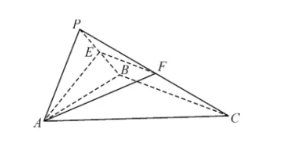
如图,在三棱锥 $P-A B C$ 中,$\triangle A B C$ 为正三角形,$P A=P B=\sqrt{6}, A B=P C=2 \sqrt{3}, E, F$分别为棱 $P B, P C$ 上的动点,且 $B C / /$ 平面 $A E F$ .
(1)证明:平面 $A B C \perp$ 平面 $P A B$ ;
(2)若截面 $A E F$ 将三棱锥 $P-A B C$ 截成上下两部分的体积之比为 $1: 3$ ,求平面 $A E F$与平面 $A B C$ 的夹角的余弦值;
(3)若球 $O$ 是三棱锥 $P-A B C$ 的外接球,若平面 $A E F$ 截球 $O$ 所得的截面的面积为 $3 \pi$ ,求 $\frac{P E}{P B}$ .
已知函数 $f(x)=(x+a) \ln x$ 有两个极值点 $x_1, x_2$ ,且 $0 < x_1 < x_2$ .
(1)求实数 $a$ 的取值范同;
(2)证明:$\frac{1}{2 x_2}+\frac{1}{x_1}>\frac{3}{2 a}$ ;
(3)证明:$\frac{\ln (n+1)}{3}>\frac{1}{5}+\frac{1}{8}+\frac{1}{11}+\cdots+\frac{1}{3 n+2}\left(n \in \mathbf{N}^*\right)$ .