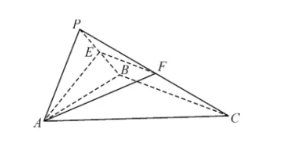
如图,在三棱锥 $P-A B C$ 中,$\triangle A B C$ 为正三角形,$P A=P B=\sqrt{6}, A B=P C=2 \sqrt{3}, E, F$分别为棱 $P B, P C$ 上的动点,且 $B C / /$ 平面 $A E F$ .
(1)证明:平面 $A B C \perp$ 平面 $P A B$ ;
(2)若截面 $A E F$ 将三棱锥 $P-A B C$ 截成上下两部分的体积之比为 $1: 3$ ,求平面 $A E F$与平面 $A B C$ 的夹角的余弦值;
(3)若球 $O$ 是三棱锥 $P-A B C$ 的外接球,若平面 $A E F$ 截球 $O$ 所得的截面的面积为 $3 \pi$ ,求 $\frac{P E}{P B}$ .