一、单选题 (共 7 题,每小题 5 分,共 50 分,每题只有一个选项正确)
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 上连续, 其导函数图形如图所示, 则 $f(x)$ 的极值点的个数为
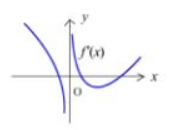
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
$\lim _{x \rightarrow 0} \frac{\int_0^{x^2} \sin t^2 \mathrm{~d} t}{x^6}=$
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $1$
当 $x \rightarrow 0$ 时, $\mathrm{e}^x-\frac{1+a x^2}{1+b x}$ 与 $x^3$ 是同阶无穷小, 则
$\text{A.}$ $a=\frac{1}{2}, b=1$.
$\text{B.}$ $a=-\frac{1}{2}, b=1$.
$\text{C.}$ $a=\frac{1}{2}, b=-1$.
$\text{D.}$ $a=-\frac{1}{2}, b=-1$.
设级数 $\sum_{n=1}^{\infty} a_n x^n$ 在 $x=1$ 处条件收敛, 且 $\lim _{n \rightarrow \infty} \frac{a_{n+1}}{a_n}=a$ 存在, 则
$\text{A.}$ $a=1$.
$\text{B.}$ $a=-1$.
$\text{C.}$ $a < 1$
$\text{D.}$ $a>1$.
设 $f(x)=\ln \left(1+x^{\frac{2}{3}}\right)-x^{\frac{2}{3}}$, 则
$\text{A.}$ $f^{\prime}(0)$ 不存在, $f^{\prime \prime}(0)$ 不存在.
$\text{B.}$ $f^{\prime}(0)$ 存在, $f^{\prime \prime}(0)$ 不存在.
$\text{C.}$ $f^{\prime}(0)$ 存在, $f^{\prime \prime}(0)$ 存在.
$\text{D.}$ 无法确定 $f^{\prime \prime}(0)$ 是否存在.
$x \rightarrow 0^{+}$时, 下列无穷小量的阶数从低到高的排序是
① 由 $\left\{\begin{array}{l}x=t^3 \\ y=t^2\end{array}\right.$ 确定的函数 $y=f(x)$
②$\ln \left(-x+\sqrt{1+x^2}\right)$
③$\int_0^{\sin x} \ln \left(1+\sqrt{t^2}\right) \mathrm{d} t$
④$\frac{1-\cos \sqrt{x}}{\sqrt[4]{x}}$
$\text{A.}$ ①④②③
$\text{B.}$ ②④①③
$\text{C.}$ ①④③②
$\text{D.}$ ④②①③
函数 $f(x)=\left\{\begin{array}{ll}1+x^2 & x \leq 0 \\ x-2 & x>0\end{array}\right.$ 是
$\text{A.}$ 在 $(-\infty,+\infty)$ 单调增加函数
$\text{B.}$ 在 $(-\infty,+\infty)$ 单调减少函数
$\text{C.}$ 在 $(-\infty, 0)$ 单增 $(0,+\infty)$ 单减函数
$\text{D.}$ 在 $(-\infty, 0)$ 单减 $(0,+\infty)$ 单增函数
二、填空题 (共 4 题, 每小题 5 分,共 20 分, 请把答案直接填写在答题纸上)
设 $f(x)=\int_{-x}^x \frac{\sin x t}{t} \mathrm{~d} t, x \neq 0$, 则 $\int x^2 f^{\prime}(x) \mathrm{d} x=$
计算极限 $\lim _{x \rightarrow 0} \frac{\left(1+x^2\right)^2-\cos x}{\sin ^2 x}$.
设数列 $\left\{a_n\right\}$ 满足 $a_0=1, a_{n+1}=\sin a_n$, 则幂级数 $\sum_{n=1}^{\infty}\left(a_n+\frac{1}{n}\right) x^n$ 的收敛域为
求极限 $\lim _{n \rightarrow \infty} \frac{1}{n^2}\left(\sqrt[3]{n^2}+\sqrt[3]{2 n^2}+\cdots+\sqrt[3]{n \cdot n^2}\right)=$
三、解答题 ( 共 3 题,满分 80 分,解答过程应写出必要的文字说明、证明过程或演算步骤 )
设 $f(x)$ 是定义在 $\mathbb{R}$ 上且以 $T>0$ 为周期的连续函数, 证明:
$$
\lim _{n \rightarrow \infty} n \int_n^{+\infty} \frac{f(x)}{x^2} \mathrm{~d} x=\frac{1}{T} \int_0^T f(x) \mathrm{d} x
$$
设 $f(x)$ 在 $x=0$ 处二阶可导, 且 $\lim _{x \rightarrow 0} \frac{f(x)}{x}=1, \lim _{x \rightarrow 0}\left(\frac{f(x)}{\sin x}\right)^{\frac{1}{f(x)}}=\sqrt{e}$, 求 $f^{\prime \prime}(0)$ 的 值.
$\lim _{x \rightarrow \infty}\left(\sin \frac{1}{x}+\cos \frac{1}{x}\right)^x$