解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图, 直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 的底面 $A B C D$ 为平行四边形, $\angle D A B=\frac{\pi}{3}, 3 A D=$ $2 C D=2 D D_1=6$, 点 $P, M$ 分别为 $A B, C D_1$ 上靠近 $A, D_1$ 的三等分点.
(1) 求点 $M$ 到直线 $P D_1$ 的距离; 来源: 高三答案公众号
(2) 求直线 $P D$ 与平面 $P C D_1$ 所成角的正弦值.

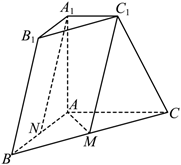
三棱台 $A B C-A_1 B_1 C_1$ 中, 若 $A_1 A \perp$ 面 $A B C, A B \perp A C, A B=A C=A A_1=2, A_1 C_1=1$, $M, N$ 分别是 $B C, B A$ 中点.
(1) 求证: $A_1 N / /$ 平面 $C_1 M A$;
(2) 求平面 $C_1 M A$ 与平面 $A C C_1 A_1$ 所成夹角的余弦值;
如图, 在直三棱柱 $A B C-A_1 B_1 C_1$ 中, $A B=A C=A A_1=2, \angle B A C=90^{\circ}, E, F$ 依次为 $C_1 C, B C$ 的中点.
(1) 求证: $A_1 B \perp B_1 C$
(2) 求 $A_1 B$ 与平面 $A E F$ 所成角的正弦值.
