单选题 (共 4 题 ),每题只有一个选项正确
已知 $\alpha: x>1, \beta: \frac{1}{x} < 1$, 则 $\alpha$ 是 $\beta$ 的
$\text{A.}$ 必要非充分条件
$\text{B.}$ 充分非必要条件
$\text{C.}$ 充要条件
$\text{D.}$ 既非充分又非必要条件
某社区通过公益讲座宣传交通法规. 为了解讲座效果, 随机抽取 10 位居民, 分别在讲座前、后各回答一份交通法规知识问卷, 满分为 100 分.他们得分的茎叶图如图所示 ("叶"是个位数字), 则下列选项叙述错误的是
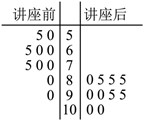
$\text{A.}$ 讲座后的答卷得分整体上高于讲座前的得分
$\text{B.}$ 讲座前的答卷得分分布较讲座后分散
$\text{C.}$ 讲座后答卷得分的第80百分位数为95
$\text{D.}$ 讲座前答卷得分的极差大于讲座后得分的极差
对于函数 $f(x)=\sqrt{3} \sin x \cos x+\sin ^2 x-\frac{1}{2}$, 给出下列结论:
(1) 函数 $y=f(x)$ 的图像关于点 $\left(\frac{5 \pi}{12}, 0\right)$ 对称;
(2) 函数 $y=f(x)$ 在区间 $\left[\frac{\pi}{6}, \frac{2 \pi}{3}\right]$ 上的值域为 $\left[-\frac{1}{2}, 1\right]$;
(3) 将函数 $y=f(x)$ 的图像向左平移 $\frac{\pi}{3}$ 个单位长度得到函数 $y=-\cos 2 x$ 的图像;
(4) 曲线 $y=f(x)$ 在 $x=\frac{\pi}{4}$ 处的切线的斜率为 1 .则所有正确的结论是
$\text{A.}$ $(1) (2)$
$\text{B.}$ $(2)(3)$
$\text{C.}$ $(2)(4)$
$\text{D.}$ $(1) (3)$
设 $P$ 为曲线 $C: y^2=4 x$ 上的任意一点, 记 $P$ 到 $C$ 的准线的距离为 $d$. 若关于点集 $A=\{M|| M P \mid=d\}$ 和 $B=\left\{(x, y) \mid(x-1)^2+(y-1)^2=r^2\right\}$ ,给出如下结论:
(1)任意 $r \in(0,+\infty), A \cap B$ 中总有 2 个元素;
(2)存在 $r \in(0,+\infty)$, 使得 $A \cap B=\varnothing$.其中正确的是
$\text{A.}$ (1)成立,(2)成立
$\text{B.}$ (1)不成立,(2)成立
$\text{C.}$ (1)成立, (2)不成立
$\text{D.}$ (1)不成立,(2)不成立
填空题 (共 12 题 ),请把答案直接填写在答题纸上
已知 i 为虚数单位, 复数 $z=\mathrm{i}(1+3 \mathrm{i})$,则 $|\bar{z}|=$
若抛物线 $y^2=-2 p x$ 过点 $(-1,2)$, 则该抛物线的焦点为
二项式 $\left(1-\frac{1}{x}\right)(1+x)^6$ 展开式中 $x^3$ 的系数为
已知两个正数 $a, b$ 的几何平均值为 1 , 则 $a^2+b^2$ 的最小值为
已知随机变量 $X \sim B(50, p)$, 且 $E[X]=20$ ,则 $D[X]=$
4 名志愿者全部分到 3 所学校支教, 要求每所学校至少有 1 名志愿者, 则不同的分法共有 $\qquad$种.
现有一个底面半径为 2 cm 、高为 9 cm 的圆柱形铁料, 若将其熔铸成一个球形实心工件,则该工件的表面积为 $\qquad$ $\mathrm{cm}^2$ (损耗忽略不计).
已知随机变量 $X$ 服从正态分布 $N(0,1)$,若 $P(X < -1.96)=0.03$, 则 $P(|X| < 1.96)=$
方程 $\lg (-2 x)=\lg \left(3-x^2\right)$ 的解集为
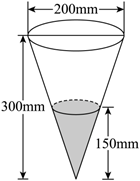
对24小时内降水在平地上的积水厚度(mm) 进行如下定义:

小明用了一个圆锥形容器接了 24 小时的雨水, 则这一天的雨水属于等级 $\qquad$ . (只填入雨水等级所对应的序号)
已知 ${a}=(-2,-1), {b}=(-4, m)$, 若向量 ${b}$在向量 $a$ 方向上的数量投影为 $\sqrt{5}$ ,则实数 $m=$
若 $F_1 、 F_2$ 是双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$的左右焦点, 过 $F_1$ 的直线 $l$ 与双曲线的左右两支分别交于 $\mathrm{A}, B$ 两点. 若 $\triangle A B F_2$ 为等边三角形, 则双曲线的离心率为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 角 $A 、 B 、 C$ 所对边的边长分别为 $a 、 b 、 c$, 已知 $a=2 \sqrt{2}, C=45^{\circ}$.
(1) 若 $\sin A=\sqrt{2} \sin B$, 求 $C$;
(2) 若 $B-A=15^{\circ}$, 求 $\mathrm{V} A B C$ 的面积.
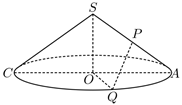
如图, 已知顶点为 S 的圆锥其底面圆 $O$ 的半径为 8 , 点 $Q$ 为圆锥底面半圆弧 $A C$ 的中点,点 $P$ 为母线 $S A$ 的中点.
(1) 若母线长为 10 , 求圆锥的体积;
(2) 若异面直线 $P Q$ 与 $S O$ 所成角大小为 $\frac{\pi}{4}$, 求 $P 、 Q$ 两点间的距离.
2021年国庆期间,某县书画协会在县宣传部门的领导下组织了庆国庆书画展,参展的 200 幅书画作品反映了该县人民在党的领导下进行国家建设中的艰苦卓绝,这些书画作品的作者的年龄都在 $[25,85]$ 之间,根据统计结果, 作出如图所示的频率分布直方图:
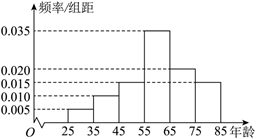
(1) 求这 200 位作者年龄的平均数 $\bar{x}$ 和方差 $s^2$ (同一组数据用该区间的中点值作代表);
(2) 县委宣传部从年龄在 $[35,45)$ 和 $[65,75)$ 的作者中, 按照分层抽样的方法, 抽出 6 人参加县委组织的表彰大会,现要从 6 人中选出 3 人作为代表发言,设这 3 位发言者的年龄落在区间 $[35,45)$ 的人数是 $X$ ,求变量 $X$ 的分布列和数学期望。
设椭圆 $\Gamma: \frac{x^2}{a^2}+y^2=1(a>1), \Gamma$ 的离心率是短轴长的 $\frac{\sqrt{2}}{4}$ 倍, 直线 $l$ 交 $\Gamma$ 于 $A 、 B$ 两点, $C$ 是 $\Gamma$ 上
异于 $A 、 B$ 的一点, $O$ 是坐标原点.
(1)求椭圆 $\Gamma$ 的方程;
(2)若直线$l$过$\Gamma$的右焦点$F$,且$ \vec{CO}=\vec{OB}, \vec{CF} \cdot \vec{AB}=0$,求$S_{\triangle CBF}$ 的值
(3)设直线 $l$ 的方程为 $y=k x+m(k, m \in \mathrm{R})$ ,且 $\overrightarrow{O A}+\overrightarrow{O B}=\overrightarrow{C O}$ ,求 $|\overrightarrow{A B}|$ 的取值范围.
已知函数 $f(x)=\frac{1}{2} x^2-(a+1) x+a \ln x$. (其中 $a$ 为常数)
(1) 若 $a=-2$, 求曲线 $y=f(x)$ 在点 $(2, f(2))$ 处的切线方程;
(2) 当 $\mathrm{a} < 0$ 时, 求函数 $y=f(x)$ 的最小值;
(3) 当 $0 \leq a < 1$ 时, 试讨论函数 $y=f(x)$ 的零点个数, 并说明理由.