解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在平面直角坐标系 $x O y$ 中,已知抛物线 $y=x^2-2 t x+t^2-t$.
(1)求抛物线的顶点坐标(用含暏代数式表示);
(2) 点 $P\left(x_1, y_1\right), Q\left(x_2, y_2\right)$ 在抛物线上,其中 $t-1 \leq x_1 \leq t+2, x_2=1-t$.
①若 $y_1$ 的最小值是 -2 ,求 $y_1$ 的最大值;
②若对于 $x_1, x_2$ ,都有 $y_1 < y_2$ ,直接写出的取值范围.
如图,圆内接四边形 $A B C D$ 的对角线 $A C , B D$ 交于点 $E, B D$ 平分 $\angle A B C , \angle B A C=\angle A D B$.
(1)求证 $D B$ 平分 $\angle A D C$ ,并求 $\angle B A D$ 的大小;
(2)过点 $C$ 作 $C F \| A D$ 交 $A B$ 的延长线于点 $F$. 若 $A C=A D, B F=2$ ,求此圆半径的长.

如图, 在 $\triangle A B C$ 中, $A B=A C, \odot O$ 是 $\triangle A B C$ 的外接圆, 过点 $O$ 作 $A C$ 的垂线,垂足为 $D$, 分别交直线 $B C, \overparen{A C}$ 于点 $E, F$, 射线 $A F$ 交直线 $B C$ 于点 $G$.
(1) 求证 $A C=C G$.
(2) 若点 $E$ 在 $C B$ 的延长线上, 且 $E B=C G$, 求 $\angle B A C$ 的度数.
(3)当 $B C=6$ 时, 随着 $C G$ 的长度的增大, $E B$ 的长度如何变化? 请描述变化过程, 并说明理由。

已知二次函数 $y=a x^2-2 a x+3$ ( $a$ 为常数, $a \neq 0$ ).
(1) 若 $a < 0$, 求证: 该函数的图象与 $x$ 轴有两个公共点.
(2) 若 $a=-1$, 求证: 当 $-1 < x < 0$ 时, $y>0$.
(3) 若该函数的图象与 $x$ 轴有两个公共点 $\left(x_1, 0\right),\left(x_2, 0\right)$, 且 $-1 < x_1 < x_2 < 4$, 则 $a$ 的取值范围是
如图, 四边形 $A B C D$ 中, $A D \| B C, \angle A B C=60^{\circ}, A D=A B=2, B C=4, E$ 为射线 $C B$ 上的动点, 将线段 $A E$ 绕 $A$ 点顺时针旋转 $120^{\circ}$ 得到 $A E^{\prime}$. 设 $C E=x, \triangle B E E^{\prime}$ 的面积为 $S$.
(1)当 $x=3$ 时, 求 $B E^{\prime}$ 的长;
(2)当 $x \neq 4$ 时, 求 $S$ 关于 $x$ 的函数表达式;
(3)求 $D E^{\prime}$ 的最小值.

在平面直角坐标系中, 二次函数 $y=-\frac{1}{4} x^2+b x+c$ 的图象与 $x$ 轴交于 $A 、 B$ 两点, $A(-2,0)$, 与 $y$ 轴交于点 $C(0$, $2)$, 点 $P$ 为函数图象上的动点.
(1) 求这个二次函数的表达式;
(2) 当点 $P$ 的横坐标为 6 时, 求 $\triangle B C P$ 的面积;
(3) 若点 $P$ 关于直线 $B C$ 的对称点 $P^{\prime}$ 恰好落在 $y$ 轴上, 求点 $P$ 的坐标.
已知点 $E$ 是正方形 $A B C D$ 内部一点, 且 $\angle B E C=90^{\circ}$.
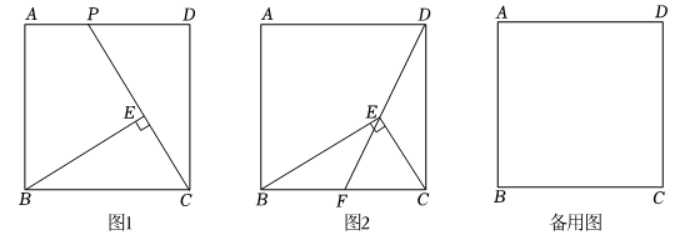
【初步探究】
(1) 如图1, 延长 $C E$ 交 $A D$ 于点 $P$. 求证: $\triangle B E C \sim \triangle C D P$;
【深入探究】
(2) 如图2, 连接 $D E$ 并延长交 $B C$ 于点 $F$, 当点 $F$ 是 $B C$ 的中点时, 求 $\frac{C E}{B E}$ 的值;
【延伸探究】
(3) 连接 $D E$ 并延长交 $B C$ 于点 $F, D F$ 把 $\angle B E C$ 分成两个角, 当这两个角的度数之比为 $1: 2$ 时, 请直接写出 $\frac{C E}{B E}$ 的值.