已知点 $E$ 是正方形 $A B C D$ 内部一点, 且 $\angle B E C=90^{\circ}$.


【初步探究】
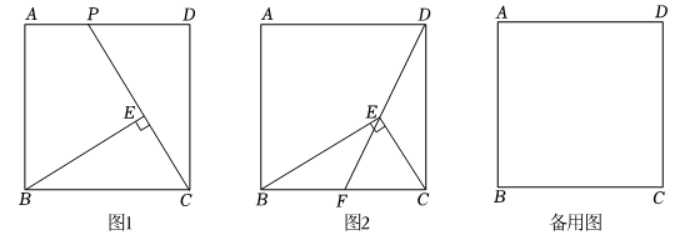
(1) 如图1, 延长 $C E$ 交 $A D$ 于点 $P$. 求证: $\triangle B E C \sim \triangle C D P$;

【深入探究】
(2) 如图2, 连接 $D E$ 并延长交 $B C$ 于点 $F$, 当点 $F$ 是 $B C$ 的中点时, 求 $\frac{C E}{B E}$ 的值；

【延伸探究】
(3) 连接 $D E$ 并延长交 $B C$ 于点 $F, D F$ 把 $\angle B E C$ 分成两个角, 当这两个角的度数之比为 $1: 2$ 时, 请直接写出 $\frac{C E}{B E}$ 的值.