单选题 (共 4 题 ),每题只有一个选项正确
已知实数 $a>0, b < 0$, 则 $\frac{\sqrt{3} b-a}{\sqrt{a^2+b^2}}$ 的取值范围是
$\text{A.}$ $[-2,-1)$
$\text{B.}$ $(-2,-1)$
$\text{C.}$ $(-2 .-1]$
$\text{D.}$ $[-2,-1]$
函数 $f(x)$ 的定义域为 $R$, 且 $f(2 x+1)$ 为偶函数, $f(x)=f(x+1)-f(x+2)$, 若 $f(1)=2$, 则 $f(18)=$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ -1
$\text{D.}$ -2
已知 $f(x)=x^3+6 x^2+9 x+11, f(x)$ 的一条切线 $g(x)=k x+b$ 与 $f(x)$ 有且仅有一个交点, 则
$\text{A.}$ $k=-3, b=3$
$\text{B.}$ $k=-3, b=-3$
$\text{C.}$ $k=3, b=3$
$\text{D.}$ $k=3, b=-3$
有很多立体图形都体现了数学的对称美, 其中半正多面体是由两种或两种以上的正多边形围成的多面体, 半正多面体因其最早由阿基米德研究发现, 故也被称作阿基米德体.如图, 这是一个棱数为 24 , 棱长为 $\sqrt{2}$ 的半正多面体, 它的所有顶点都在同一个正方体的表面上, 可以看成是由一个正方体截去八个一样的四面体所得.若点 $E$ 为线段 $B C$ 上的动点, 则直线 $D E$ 与直线 $A F$ 所成角的余弦值的取值范围为

$\text{A.}$ $\left[\frac{1}{3}, \frac{\sqrt{2}}{2}\right]$
$\text{B.}$ $\left[\frac{1}{3}, \frac{\sqrt{3}}{2}\right]$
$\text{C.}$ $\left[\frac{1}{2}, \frac{\sqrt{2}}{2}\right]$
$\text{D.}$ $\left[\frac{1}{2}, \frac{\sqrt{3}}{2}\right]$
多选题 (共 2 题 ),每题有多个选项正确
已知事件 $A, B$ 满足 $P(A)=0.5, P(B)=0.2$, 则
$\text{A.}$ 若 $B \subseteq A$, 则 $P(A B)=0.5$
$\text{B.}$ 若 $A$ 与 $B$ 互斥, 则 $P(A+B)=0.7$
$\text{C.}$ 若 $A$ 与 $B$ 相互独立, 则 $P(A \bar{B})=0.9$
$\text{D.}$ 若 $P(B \mid A)=0.2$, 则 $A$ 与 $B$ 相互独立
已知随机变量 $\mathrm{X}$ 的概率密度函数为 $\varphi(x)=\frac{1}{\sqrt{2 \pi} a} e^{-\frac{(x-b)^2}{2 a^2}}(a>0, b>0)$, 且 $\varphi(x)$ 的极大值点为 $x=2 a$,记 $f(k)=P(X < k), g(k)=P(X>k+a)$, 则
$\text{A.}$ $X \sim N(b, a)$
$\text{B.}$ $X \sim N\left(2 a, a^2\right)$
$\text{C.}$ $f(a)=g(2 a)$
$\text{D.}$ $f(2 a)+g(2 a)=f(a)+g(a)$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
数论领域的四平方和定理最早由欧拉提出, 后被拉格朗日等数学家证明. 四平方和定理的内容是: 任意正整数都可以表示为不超过四个自然数的平方和, 例如正整数 $12=3^2+1^2+1^2+1^2=2^2+2^2+2^2+0^2$. 设 $25=a^2+b^2+c^2+d^2$, 其中 $a, b, c, d$ 均为自然数, 则满足条件的有序数组 $(a, b, c, d)$ 的个数是
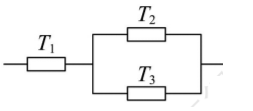
三个元件 $a, b, c$ 独立正常工作的概率分别是 $P_1, P_2$, $P_3\left(0 < P_1 < P_2 < P_3 < 1\right)$, 把它们随意接入如图所示电路的三个盒 $T_1, T_2, T_3$ 中 (一盒接一个元件), 各种连接方法中, 此电路工作的最大概率是
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left\{a_n\right\},\left\{b_n\right\}$ 满足 $a_1=-2 b_1=4$, 且 $\left\{a_n\right\}$ 是公差为 1 的等差数列, $\left\{a_n+b_n\right\}$ 是公比为 2 的等比数列.
(1) 求 $\left\{a_n\right\},\left\{b_n\right\}$ 的通项公式;
(2) 求 $\left\{\left|b_n\right|\right\}$ 的㷙 $n$ 项和 $T_n$.
某百科知识竞答比赛的半决赛阶段, 每两人一组进行 $P K$, 胜者晋级决赛, 败者终止比赛. 比赛最多有三局, 第一局限时答题, 第二局快问快答, 第三局抢答.比赛双方首先各自进行一局限时答题, 依据答对题目数量, 答对多者获胜, 比赛结束, 答对数量相等视为平局, 则需进入快问快答局; 若快问快答平局, 则需进入抢答局, 两人进行抢答, 抢答没有平局. 已知甲、乙两位选手在半决赛相遇, 且在与乙选手的比赛中, 甲限时答题局获胜与平局的概率分别为 $\frac{1}{3}, \frac{1}{2}$, 快问快答局获胜与平局的概率分别为 $\frac{1}{3}, \frac{1}{6}$, 抢答局获胜的概率为 $\frac{1}{3}$, 且各局比赛相互独立.
(1) 求甲至多经过两局比赛晋级决赛的概率;
(2) 知乙最后晋级决赛, 但不知甲、乙两人经过几局比赛, 求乙恰好经过三局比赛才晋级决赛的概率.
已知 $F_1(-\sqrt{6}, 0), F_2(\sqrt{6}, 0)$ 为双曲线 $C$ 的焦点, 点 $P(2,-1)$ 在 $C$ 上.
(1)求 $C$ 的方程;
(2) 点 $A, B$ 在 $C$ 上, 直线 $P A, P B$ 与 $y$ 轴分别相交于 $M, N$ 两点, 点 $Q$ 在直线 $A B$ 上, 若 $\overrightarrow{O M}+\overrightarrow{O N}=\overrightarrow{0}$, $\overrightarrow{P Q} \cdot \overrightarrow{A B}=0$, 是否存在定点 $T$, 使得 $|Q T|$ 为定值? 若有, 请求出该定点及定值; 若没有, 请说明理由。
已知函数 $f(x)=x+k \sin x$, 其中 $0 < k \leq 1$.
(1) 设函数 $g(x)=\frac{1}{2} x^2-f(x)$, 证明:
①$g(x)$ 有且仅有一个极小值点;
②记 $x_0$ 是 $g(x)$ 的唯一极小值点, 则 $g\left(x_0\right) < -\frac{1}{2} x_0$;
(2) 若 $k=1$, 直线 $l$ 与曲线 $y=f(x)$ 相切, 且有无穷多个切点, 求所有符合上述条件的直线 $l$ 的方程.