单选题 (共 12 题 ),每题只有一个选项正确
设二次函数 $y=x^2+2 a x+\frac{a^2}{2}$ 的图象的顶点为 $A$, 与 $x$ 轴的交点为 $B, C$. 当 $\triangle A B C$ 为等边三角形时, 其边长为
$\text{A.}$ $\sqrt{6}$.
$\text{B.}$ $2 \sqrt{2}$.
$\text{C.}$ $2 \sqrt{3}$.
$\text{D.}$ $3 \sqrt{2}$.
如图, 在矩形 $A B C D$ 中, $\angle B A D$ 的平分线交 $B D$ 于点 $E, A B=1, \angle C A E=15^{\circ}$, 则 $B E=$
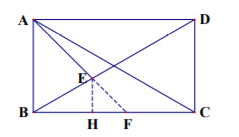
$\text{A.}$ $\frac{\sqrt{3}}{3}$.
$\text{B.}$ $\frac{\sqrt{2}}{2}$.
$\text{C.}$ $\sqrt{2}-1$.
$\text{D.}$ $\sqrt{3}-1$.
设 $p, q$ 均为大于 3 的素数, 则使 $p^2+5 p q+4 q^2$ 为完全平方数的素数对 $(p, q)$ 的个数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
若实数 $a, b$ 满足 $a-b=2, \frac{(1-a)^2}{b}-\frac{(1+b)^2}{a}=4$, 则 $a^5-b^5=$
$\text{A.}$ 46 .
$\text{B.}$ 64 .
$\text{C.}$ 82 .
$\text{D.}$ 128.
对任意的整数 $x, y$, 定义 $x @ y=x+y-x y$, 则使得 $(x @ y) @ z+(y @ z) @ x+(z @ x) @ y$ $=0$ 的整数组 $(x, y, z)$ 的个数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
设 $M=\frac{1}{2018}+\frac{1}{2019}+\frac{1}{2020}+\cdots+\frac{1}{2050}$, 则 $\frac{1}{M}$ 的整数部分是
$\text{A.}$ 60
$\text{B.}$ 61
$\text{C.}$ 62
$\text{D.}$ 63
满足 $\left(x^2+x-1\right)^{x+2}=1$ 的整数 $x$ 的个数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
已知 $x_1, x_2, x_3\left(x_1 < x_2 < x_3\right)$ 为关于 $x$ 的方程 $x^3-3 x^2+(a+2) x-a=0$ 的三个实数根, 则 $4 x_1-x_1^2+x_2^2+x_3^2=$
$\text{A.}$ 5
$\text{B.}$ 6
$\text{C.}$ 7
$\text{D.}$ 8
已知点 $E, F$ 分别在正方形 $A B C D$ 的边 $C D, A D$ 上, $C D=4 C E, \angle E F B=\angle F B C$, 则 $\tan \angle A B F=$
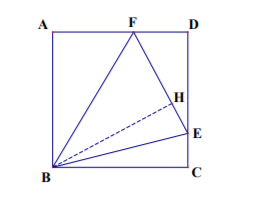
$\text{A.}$ $\frac{1}{2}$.
$\text{B.}$ $\frac{3}{5}$.
$\text{C.}$ $\frac{\sqrt{2}}{2}$.
$\text{D.}$ $\frac{\sqrt{3}}{2}$.
方程 $\sqrt{3+\sqrt{9+x}}=\sqrt[3]{x}$ 的实数根的个数为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
设 $a, b, c$ 为三个实数, 它们中任何一个数加上其余两数之积的 2017 倍都等于 2018 , 则这样的三元数组 $(a, b, c)$ 的个数为
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ 7
已知实数 $a, b$ 满足 $a^3-3 a^2+5 a=1, b^3-3 b^2+5 b=5$, 则 $a+b=$
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
填空题 (共 8 题 ),请把答案直接填写在答题纸上
如图, 在平行四边形 $A B C D$ 中, $B C=2 A B, C E \perp A B$ 于 $E, F$ 为 $A D$ 的中点, 若 $\angle A E F=48^{\circ}$,则 $\angle B=$
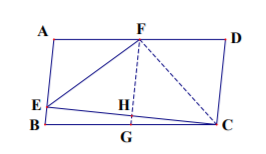
若实数 $x, y$ 满足 $x^3+y^3+\frac{1}{4}(x+y)=\frac{15}{2}$, 则 $x+y$ 的最大值为
已知实数 $a, b, c$ 满足 $a+b+c=0, a^2+b^2+c^2=1$, 则 $\frac{a^5+b^5+c^5}{a b c}=$
已知 $p, q, r$ 为素数, 且 $p q r$ 整除 $p q+q r+r p-1$, 则 $p+q+r=$
已知两个正整数的和比它们的积小 1000 , 若其中较大的数是完全平方数, 则较小的数为
已知 $D$ 是 $\triangle A B C$ 内一点, $E$ 是 $A C$ 的中点, $A B=6, B C=10, \angle B A D=\angle B C D$, $\angle E D C=\angle A B D$, 则 $D E=$
已知二次函数 $y=x^2+2(m+2 n+1) x+\left(m^2+4 n^2+50\right)$ 的图象在 $x$ 轴的上方, 则满足条件的正整数对 $(m, n)$ 的个数为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $a, b, c, d$ 为四个不同的实数, 若 $a, b$ 为方程 $x^2-10 c x-11 d=0$ 的根, $c, d$为方程 $x^2-10 a x-11 b=0$ 的根, 求 $a+b+c+d$ 的值.
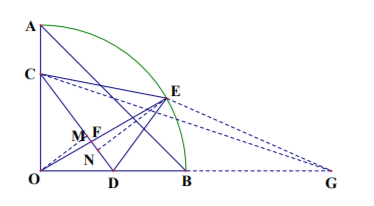
如图, 在扇形 $O A B$ 中, $\angle A O B=90^{\circ}, O A=12$, 点 $C$ 在 $O A$ 上, $A C=4$,点 $D$ 为 $O B$ 的中点, 点 $E$ 为弧 $A B$ 上的动点, $O E$ 与 $C D$ 的交点为 $F$.
(1) 当四边形 $O D E C$ 的面积 $S$ 最大时, 求 $E F$;
(2) 求 $C E+2 D E$ 的最小值.
求所有的正整数 $m, n$, 使得 $\frac{m^3+n^3-m^2 n^2}{(m+n)^2}$ 是非负整数.
若实数 $a, b, c$ 满足 $(a+b+c)\left(\frac{1}{a+b-5 c}+\frac{1}{b+c-5 a}+\frac{1}{c+a-5 b}\right)=\frac{9}{5}$, 求 $(a+b+c)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)$ 的值.
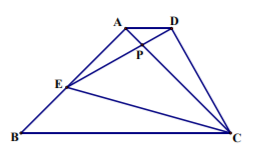
如图, 点 $E$ 在四边形 $A B C D$ 的边 $A B$ 上, $\triangle A B C$ 和 $\triangle C D E$ 都是等腰直角三角形, $A B=A C, D E=D C$.
(1) 证明: $A D / / B C$; (2) 设 $A C$ 与 $D E$ 交于点 $P$, 如果 $\angle A C E=30^{\circ}$, 求 $\frac{D P}{P E}$.
设 $x$ 是一个四位数, $x$ 的各位数字之和为 $m, x+1$ 的各位数字之和为 $n$, 并且 $m$ 与 $n$ 的最大公约数是一个大于 2 的素数. 求 $x$.