单选题 (共 12 题 ),每题只有一个选项正确
若 $\mathrm{i} z=1+\mathrm{i}$, 则复数 $z=$
$\text{A.}$ $1+\mathrm{i}$
$\text{B.}$ $1-\mathrm{i}$
$\text{C.}$ $-1+\mathrm{i}$
$\text{D.}$ $-1-\mathrm{i}$
已知 $A=\left\{x \mid x^2-x < 0\right\}, B=\{x \mid x < 2\}$, 则 $A \cap B=$
$\text{A.}$ $(0,1)$
$\text{B.}$ $(0,2)$
$\text{C.}$ $(1,2)$
$\text{D.}$ $(-\infty, 2)$
已知 $\boldsymbol{a}=(1,0),|\boldsymbol{b}|=1,|\boldsymbol{a}-\boldsymbol{b}|=\sqrt{3}$, 则 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 的夹角为
$\text{A.}$ $\frac{\pi}{6}$
$\text{B.}$ $\frac{\pi}{3}$
$\text{C.}$ $\frac{2 \pi}{3}$
$\text{D.}$ $\frac{5 \pi}{6}$
若变量 $x, y$ 满足不等式组 $\left\{\begin{array}{l}x \geqslant 0, \\ 2 x+y-2 \leqslant 0,\end{array}\right.$ 则 $x+y$ 的最大值是
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ 1
$\text{D.}$ 2
已知变量 $x, y$ 之间的线性回归方程为 $\hat{y}=2 x+1$, 且变量 $x, y$ 之间的一组相关数据如表所示,

则下列说法正确的是
$\text{A.}$ $m=17$
$\text{B.}$ 变量 $y$ 与 $x$ 是负相关关系
$\text{C.}$ 该回归直线必过点 $(5,11)$
$\text{D.}$ $x$ 增加 1 个单位, $y$ 一定增加 2 个单位
已知 $f(x)$ 为 $\mathbf{R}$ 上的减函数, 则
$\text{A.}$ $f\left(0.2^{-0.3}\right)>f\left(\log _3 2\right)>f(0.5)$
$\text{B.}$ $f(0.5)>f\left(\log _3 2\right)>f\left(0.2^{-0.3}\right)$
$\text{C.}$ $f\left(\log _3 2\right)>f(0.5)>f\left(0.2^{-0.3}\right)$
$\text{D.}$ $f\left(0.2^{-0.3}\right)>f(0.5)>f\left(\log _3 2\right)$
已知 $x>0, y>0$, 则 “ $x+y \leqslant 1$ ” 是 “ $x^2+y^2 \leqslant 1$ ” 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知角 $\alpha$ 的终边与角 $\beta$ 的终边关于 $y=x$ 对称 ( $\beta$ 为象限角), 则 $\frac{\cos (\alpha-\beta)}{\sin 2 \beta}=$
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ 1
$\text{D.}$ 2
如右图是 $y=f(x)$ 的大致图象, 则 $f(x)$ 的解析式可能为
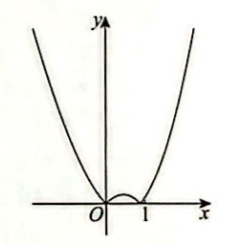
$\text{A.}$ $f(x)=\left|x^2-\sin x\right|$
$\text{B.}$ $f(x)=|x-\sin x|$
$\text{C.}$ $f(x)=\left|2^x-1\right|$
$\text{D.}$ $f(x)=\left|x^2-x-\frac{1}{4}\right|$
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $S_n=\frac{3^n-2}{3^n}$, 则下列说法正确的是
$\text{A.}$ $a_n < a_{n+1}$
$\text{B.}$ $S_n>S_{n+1}$
$\text{C.}$ $a_n+2 S_n=1$
$\text{D.}$ $0 < a_n \leqslant \frac{4}{9}$
已知曲线 $y=x^2-2 m x+m-1$ 与 $x$ 轴交于不同的两点 $A, B$, 与 $y$ 轴交于点 $C$, 则过 $A$, $B, C$ 三点的圆的圆心轨迹为
$\text{A.}$ 直线
$\text{B.}$ 圆
$\text{C.}$ 椭圆
$\text{D.}$ 双曲线
设 $F_1, F_2$ 分别为椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左, 右焦点, 以 $F_1$ 为圆心且过 $F_2$ 的圆与 $x$ 轴交于另一点 $P$, 与 $y$ 轴交于点 $Q$, 线段 $Q F_2$ 与 $C$ 交于点 $A$. 已知 $\triangle A P F_2$ 与 $\triangle Q F_1 F_2$ 的面积之比为 $3: 2$, 则该椭圆的离心率为
$\text{A.}$ $\frac{2}{3}$
$\text{B.}$ $\sqrt{13}-3$
$\text{C.}$ $\sqrt{3}-1$
$\text{D.}$ $\frac{\sqrt{3}+1}{4}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知 $\alpha$ 为锐角, $\sin \alpha=\frac{4}{5}$, 则 $\sin \left(\alpha+\frac{\pi}{4}\right)=$
若 $f(x)=\ln \left(1+\frac{1}{x+b}\right)$ 为奇函数, 则 $b=$
甲、乙二人用 4 张不同的扑克牌(其中红桃 3 张,方片 1 张)玩游戏,他们将扑克牌洗匀后, 背面朝上放在案面上, 甲先抽, 乙后抽, 抽出的牌不放回, 各抽一张. 则甲、乙二人抽到的花色相同的概率为
已知 $F_1(-c, 0), F_2(c, 0)$ 分别是双曲线 $E: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左, 右焦点, 过 $F_2$ 作 $E$ 的浙近线的垂线, 垂足为 $P$. 点 $M$ 在 $E$ 的左支上, 当 $P M / / x$ 轴时, $|P M|=c$, 则 $E$ 的浙近线方程为
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $S_5=45, S_6=60$.
(1) 求 $\left\{a_n\right\}$ 的通项公式;
(2) 求数列 $\left\{\frac{1}{a_n a_{n+1}}\right\}$ 的前 $n$ 项和 $T_n$.
绵阳市 37 家 $\mathrm{A}$ 级旅游景区, 在 2023 年国庆中秋双节期间, 接待人数和门票收入大幅增长. 绵阳某旅行社随机调查了市区 100 位市民平时外出旅游情况, 得到的数据如下表:
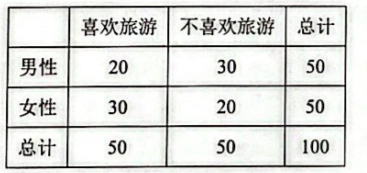
(1) 能否有 $95 \%$ 的把握认为喜欢旅游与性别有关?
(2) 在以上所调查的喜欢旅游的市民中,按性别进行分层抽样随机抽取 5 人, 再从这 5 人中随机抽取 2 人进行访谈, 求这两人是不同性别的概率.
$$
\text { 附: } K^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)} \text {. }
$$

在 $\triangle A B C$ 中, 内角 $A, B, C$ 的对边分别为 $a, b, c$, 且 $4 \overrightarrow{B A} \cdot \overrightarrow{B C}=3 b c \sin A=24 c$.
(1) 求 $\tan B$ 及 $a$;
(2) 若 $\triangle A B C$ 周长为 48 , 求 $\triangle A B C$ 的面积.
已知直线 $l: y=k x-2$ 与抛物线 $E: x^2=2 p y(p>0)$ 交于 $A, B$ 两点, $F$ 为 $E$ 的焦点,直线 $F A, F B$ 的斜率之和为 0 .
(1) 求 $E$ 的方程;
(2) 直线 $F A, F B$ 分别交直线 $y=-2$ 于 $M, N$ 两点, 若 $|M N| \geqslant 16$, 求 $k$ 的取值范围.
已知函数 $f(x)=2 \sin x-a x^2+3 x$.
(1) 求曲线 $f(x)$ 在 $x=0$ 处的切线方程;
(2) 若 $f(x)$ 在 $\left[-\frac{\pi}{2}, \pi\right]$ 上是单调函数, 求实数 $a$ 的取值范围.
点 $O$ 为极点, 以 $x$ 轴正半轴为极轴, 建立极坐标系.
(1) 求曲线 $C$ 极坐标方程;
(2) 若 $A, B$ 为曲线 $C$ 上的动点, 且 $O A \perp O B$, 求 $\frac{1}{|O A|^2}+\frac{1}{|O B|^2}$ 的值.
(1) 已知 $a, b, x, y$ 均为正数, 求证: $\frac{(x+y)^2}{a x^2+b y^2} \leqslant \frac{1}{a}+\frac{1}{b}$, 并指出等号成立的条件;
(2) 利用 (1) 的结论, 求函数 $f(x)=\frac{4 x^2+4 x+1}{5 x^2+4 x+2}(x>0)$ 的最大值, 并指出取最大值时 $x$ 的值.