单选题 （共 12 题 ），每题只有一个选项正确
下列各数中的无理数是
$\text{A.}$ $2i$
$\text{B.}$ $\sqrt{9}$
$\text{C.}$ $\frac{2}{9}$
$\text{D.}$ $\pi$
下列交通警告标识中, 不是轴对称图形的是
$\text{A.}$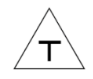 
$\text{B.}$ 
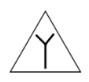$\text{C.}$ 
$\text{D.}$ 
下列调查中, 最适合全面调查的是
$\text{A.}$ 对某品牌电池的使用寿命的调查
$\text{B.}$ 对我国公民的环保意识的调查
$\text{C.}$ 对全市八年级中学生课外阅读时间的调查
$\text{D.}$ 疫情期间, 对进入公园游客的 “渝康码” 的调查
在平面直角坐标系中, 将三架形三个顶点的横坐标都乘以 -1 , 纵坐标不变, 则所得三角形与原三角形的 关系是
$\text{A.}$ 将原图向左产移一个单位
$\text{B.}$ 关于原点对称
$\text{C.}$ 关于 $x$ 轴对称
$\text{D.}$ 关于 $y$ 轴对称
若 $a>b$, 则下列式子一定成立的是
$\text{A.}$ $a < b+2$
$\text{B.}$ $1-a < 1-b$
$\text{C.}$ $a-3 < b-3$
$\text{D.}$ $\frac{a}{5} < \frac{b}{5}$
下列命题中是真命题的是
$\text{A.}$ 同位角相等
$\text{B.}$ 三角形一边的中线平分三角形的周长
$\text{C.}$ 垂直于同一直线的两直线平行
$\text{D.}$ 过直线外一点有且仅有一条直线与等直线平行
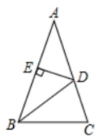
如终, 在 $\triangle A B C$ 中, $A B=A C, A D=D B, D E \perp A B$ 于点 $E$, 若 $B C=3$, 且 $\triangle B D C$ 的周长为 8 , 则 $A E$ 的长为
$\text{A.}$ 2.5
$\text{B.}$ 3
$\text{C.}$ 3.5
$\text{D.}$ 4
如图所示, 将形状、大小完全相同的 “●”和线段按照一定规律摆成下列图形, 第 1 幅图形中“●” 的 个数为 3 , 第 2 幅图形中 “●”的个数为 8 , 第 3 幅图形中 “●”的个数为 15. 以此类推, 则第 10 幅图 形中“的●个数为
$\text{A.}$ 100
$\text{B.}$ 120
$\text{C.}$ 220
$\text{D.}$ 240
如图, 在 Rt $\triangle \mathrm{ABC}$ 中, $\angle A=90^{\circ}, M$ 为 $B C$ 的中点, $H$ 为 $A B$ 上一点, 过点 $C$ 作 $C G / / A B$, 交 $H M$ 的延 长线于点 $G$, 若 $A C=10, A B=8$, 则四边形 $A C G H$ 周长的最小值是
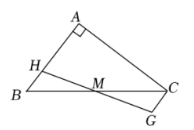
$\text{A.}$ 28
$\text{B.}$ 26
$\text{C.}$ 22
$\text{D.}$ 18
若关于 $x$ 的一元一次不等式组 $\left\{\begin{array}{l}2\left(x+\frac{1}{2}\right) \leq 2 k+1 \\ x+1>\frac{3 x-5}{2}\end{array}\right.$ 的解集是 $x \leq k$, 且关于 $y$ 的方程 $2 y=3+k$ 有正整数解, 则符合条件的所不整数 $k$ 的和为
$\text{A.}$ 5
$\text{B.}$ 8
$\text{C.}$ 9
$\text{D.}$ 15
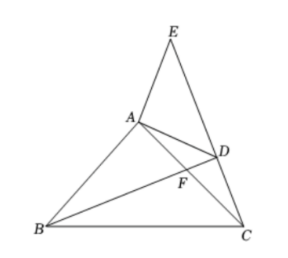
如图, 在 $\triangle A B C$ 中, 若分别以 $A B 、 A C$ 为边作 $\triangle A B D$ 和 $\triangle A C E$, 且 $\angle D A B=\angle C A E=50^{\circ}, A D=A B$, $A C=A E, D C 、 B E$ 交于点 $P$, 连接 $A P$, 则 $\angle A P D$ 的度数为 ________ 度
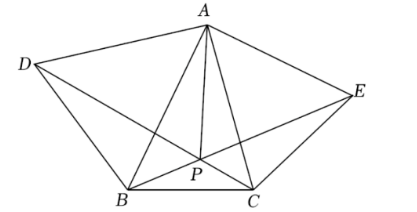
$\text{A.}$ 65
$\text{B.}$ 62.5
$\text{C.}$ 55
$\text{D.}$ 50
如图, 在 $\triangle A B C$ 中, $\angle A B C=60^{\circ}, A D$ 平分 $\angle B A C$ 交 $B C$ 于点 $D, C E$ 平分 $\angle A C B$ 交 $A B$ 于点 $E, A D$ 、 $C E$ 交于点 $F$. 则下列说法正确的个数为
(1) $\angle A F C=120^{\circ}$;
(2) $S_{\triangle A B D}=S_{A M D C}$,
(3) 若 $A B=2 A E$, 则 $C E \perp A B$;
(4) $C D+A E=A C$;
(5) $S_{\triangle A E F}: S_{\triangle F D C}=A F: F C$.
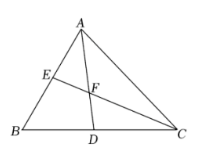
$\text{A.}$ 2个
$\text{B.}$ 3个
$\text{C.}$ 4个
$\text{D.}$ 5个
填空题 （共 13 题 ），请把答案直接填写在答题纸上
从汽车后视镜中看见某车牌的号码如图所示, 该汽车的号码实际是
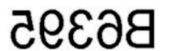
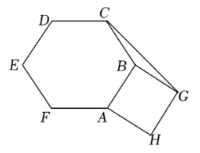
如图, 多边形 $A B C D E F$ 和多边形 $A B G H$ 分别为正六边形和正方形, 连接 $C G$, 则 $\angle C B G=$
等腰三角形的三边长分别为 $m-2,2 m+1,8$, 则等腰三角形的周长为
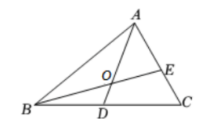
如图, 在 $\triangle A B C$ 中, 点 $D 、 E$ 分别在边 $B C 、 A C$ 上, $D$ 为 $B C$ 中点, $C E: A E=1: 2, S_{\triangle F O D}=1, S_{M O E}=\frac{8}{3}$, 则 $\triangle A B C$ 的面积为
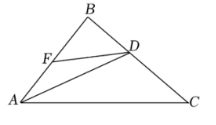
在直角三角形 $A B C$ 中, $\angle B=90^{\circ}, A D$ 为 $\angle B A C$ 的平分线, $D F=D C, \angle C=40^{\circ}$, 则 $\angle A D F=$
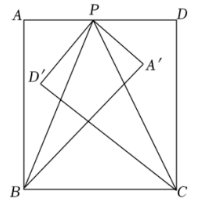
在长方形 $A B C D$ 中, 点 $P$ 在 $A D$ 上, 连接 $P B 、 P C$, 将 $\triangle A P B$ 沿 $P B$ 折得到 $\triangle A^{\prime} P B, \triangle D P C$ 沿 $P C$ 釉 折得到 $\triangle D^{\prime} P C$, 已知 $\angle D^{\prime} P B=15^{\circ}, \angle A^{\prime} P C=21^{\circ}$, 则 $\angle D^{\prime} C B$ 的度数为 ________ 度.
某医院在入口处开设了 $A 、 B 、 C$ 三种通道, 分别供本院医务人员、普通患者、老年忠者入院. $A 、 B$ 、C 通道共5个，每分钟每个通道评价可通过的人数比为 6:5:3， 该议员准备在增加三种类型的通道共5 个, 其中 $A$ 型通道增加 1 个, 受疼情防控影响, 入口通行变缓慢, 此时每分钟每个通道（包括之前的和新增的通道) 平均可通行的人数均减少 4 人, 据统计, 新增通道后, 所有通道平均每分钟可通行的 总人数比之前的总人数增加了 48 人, 且新增后所有 $B$ 型通道每分钟平均可通过的人数与新增后的总人 数之比为 $5: 9$. 那么新增通道后, 该医院所有通道平均每分钟可通行的总人数为
解方程组:
(1) $\left\{\begin{array}{l}4 x-y=10 \\ 3 x+2 y=2\end{array}\right.$;
(2) $\left\{\begin{array}{l}\frac{x}{4}+\frac{2 y}{3}=7 \\ 5 x-2(y-1)=4\end{array}\right.$
解不等式组:
(1) $\left\{\begin{array}{l}5 x-2>3(x-1) \\ x-2 \leq 14-3 x\end{array}\right.$;
(2) $\left\{\begin{array}{l}2(x-1)-x < 1 \\ \frac{x+2}{2} \geq \frac{2 x-1}{3}+1\end{array}\right.$.
如图, 在 $\triangle A B C$ 中, $\angle B A C=90^{\circ}, A B=A C$. 点 $D$ 为 $\triangle A B C$ 外一点, 连接 $B D$ 交 $A C$ 于点 $F$, 连接 $C D$, 且满足 $\angle B D C=90^{\circ}$, 适接 $A D$, 过点 $A$ 作 $A E \perp A D$ 交 $C D$ 的延长线于点 $E$.
(1) 求证: $A E=A D$;
(2) 若点 $F$ 为 $A C$ 的中点, 求证: $D E=4 D F$.
如果一个自然数 $P$ 能分解成: $P=A \times B(A < B)$, 其中 $A$ 和 $B$ 都是两位数, 且 $A$ 的十位数字与个位数字 之和与 $B$ 的十位数字与个位数字之和都为 6 , 则称 $P$ 为 “福禄数”, 把 $P$ 分解成 $P=A \times B$ 的过程叫 做 “最佳分解” .
例如: $\because 1386=33 \times 42,3+3=6,4+2=6, \therefore 1386$ 是 “福禄数”: $\because 165=11 \times 15,1+1 \neq 6 \therefore 165$ 不是 “福禄数”.
若自然数 $P$ 是 “福禄数”, “最佳分解” 为 $P=A \times B$, 记 $S(P)=2 A+4 B ; T(P)=A-B ;$ 记 $F(P)=\frac{S(P)}{T(P)}$. 又 如 : $\because P=1224=24 \times 51$ 是 “福禄数”, $\therefore S(P)=2 \times 24+4 \times 51=252$, $T(P)=24-51=-27 \therefore F(P)=\frac{S(P)}{T(P)}=\frac{252}{-27}=-\frac{28}{3}$.
(1) 判断 360 和 1890 是否是 “福禄数”? 并说明理山;
(2) 若自然数 $P$ 足 “福禄数”, 且 $F(P)$ 能被 5 整除, 求出所有满足条件的自然数 $P$.
已知 $A(a, 0), B(0, b)$ 是平画直角坐标系内的两点, 且满足 $|a+4|+(a-2 b+8)^2=0$.
(1) 直接写出 $A, B$ 两点的坐标: $A$ : $B$ :
(2) 如图 1, 如果在第二象限内有一点 $E(-2, t)$, 使得 $S_{\triangle A M E}=2 S_{\triangle A O B}$, 求点 $E$ 的坐标;
(3) 如图 2, 在 (2) 的条件下, 点 $N$ 足 $x$ 轴的上 动点, 点 $M\left(m, \frac{1}{2} m+2\right)$ 是自线 $A B$ 上一点, 足否存 在以 $E M$ 为直角边的等腰直角 $\triangle E M N$ ? 若存任, 请直接写出点 $N$ 的坐标; 若不存在, 说明理由.
