已知 $A(a, 0), B(0, b)$ 是平画直角坐标系内的两点, 且满足 $|a+4|+(a-2 b+8)^2=0$.
(1) 直接写出 $A, B$ 两点的坐标: $A$ : $B$ :
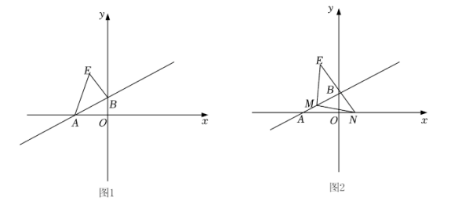
(2) 如图 1, 如果在第二象限内有一点 $E(-2, t)$, 使得 $S_{\triangle A M E}=2 S_{\triangle A O B}$, 求点 $E$ 的坐标;
(3) 如图 2, 在 (2) 的条件下, 点 $N$ 足 $x$ 轴的上 动点, 点 $M\left(m, \frac{1}{2} m+2\right)$ 是自线 $A B$ 上一点, 足否存 在以 $E M$ 为直角边的等腰直角 $\triangle E M N$ ? 若存任, 请直接写出点 $N$ 的坐标; 若不存在, 说明理由.
(1) 直接写出 $A, B$ 两点的坐标: $A$ : $B$ :
(2) 如图 1, 如果在第二象限内有一点 $E(-2, t)$, 使得 $S_{\triangle A M E}=2 S_{\triangle A O B}$, 求点 $E$ 的坐标;
(3) 如图 2, 在 (2) 的条件下, 点 $N$ 足 $x$ 轴的上 动点, 点 $M\left(m, \frac{1}{2} m+2\right)$ 是自线 $A B$ 上一点, 足否存 在以 $E M$ 为直角边的等腰直角 $\triangle E M N$ ? 若存任, 请直接写出点 $N$ 的坐标; 若不存在, 说明理由.
