解答题 (共 20 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知实数 $a, b, x, y$ 满 足 $a+b=x+y=2, a x+b y=5$, 则 $\left(a^2+b^2\right) x y+a b\left(x^2+y^2\right)=$
若 $x \neq 0$, 则 $\frac{\sqrt{1+x^2+x^4}-\sqrt{1+x^4}}{x}$ 的最大值是
若实数 $a, b, c$ 满足 $a^2+b^2+c^2=9$, 代数式 $(a-b)^2+(b-c)^2$ $+(c-a)^2$ 的最大值是
若实数 $x, y, z$ 满足 $x+\frac{1}{y}=4, y+\frac{1}{z}=1, z+\frac{1}{x}=\frac{7}{3}$, 求 $x y z$ 的值.
已知 $\frac{y+z-x}{x+y+z}=\frac{z+x-y}{y+z-x}=\frac{x+y-z}{z+x-y}=p$, 则 $p^3+p^2+p=$
求方程 $x^3+6 x^2+5 x=y^3-y+2$ 的整数解 $(x, y)$ 的个数.
设不全相等的非零实数 $a, b, c$ 满足:
$$
\frac{b c}{2 a^2+b c}+\frac{a c}{2 b^2+a c}+\frac{a b}{2 c^2+a b}=1
$$
求 $a+b+c$ 的值.
设 $x_i=\sqrt{2}-1$ 或者 $\sqrt{2}+1, i=1,2, \cdots, 2012$. 令
$$
S=x_1 x_2+x_3 x_4+\cdots+x_{2011} x_{2012} .
$$
(1) $S$ 能否等于 2013 ? 证明你的结论;
(2) $S$ 能取到多少个不同的整数值?
已知实数 $a, b, c$ 满足 $a b c=-1, a+b+c=4$,
$$
\frac{a}{a^2-3 a-1}+\frac{b}{b^2-3 b-1}+\frac{c}{c^2-3 c-1}=\frac{4}{9},
$$
求 $a^2+b^2+c^2$ 的值.
设 $n$ 是正整数, 且使得 $2^4+2^7+2^n$ 是完全平方数, 求 $n$ 的值.
已知二次函数 $y=x^2+a x+b$ 的图像与 $x$ 轴的两个交点的横坐标分 别是 $m, n$, 且 $|m|+|n| \leq 1$. 设满足上述要求的 $b$ 的最大值和最小值分 别是 $p$ 和 $q$, 则 $|p|+|q|=$
已知实数 $a, b$ 满足 $a^3-3 a^2+5 a=1, b^3-3 b^2+5 b=5$, 则 $a+b=$
设 $M=\frac{1}{2018}+\frac{1}{2019}+\frac{1}{2020}+\cdots+\frac{1}{2050}$, 则 $\frac{1}{M}$ 的整数部分是
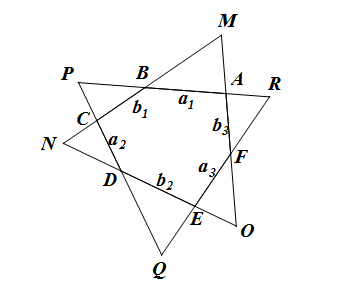
如图, $\triangle M N O$ 和 $\triangle P Q R$ 是两个全等的等边三角形. 六边形 $A B C D E F$ 的边长分别记为
$$
\begin{aligned}
& A B=a_1, B C=b_1, C D=a_2, \\
& D E=b_2, E F=a_3, F A=b_3 .
\end{aligned}
$$
求证: $a_1^2+a_2^2+a_3^2=b_1^2+b_2^2+b_3^2$.
计算: $\frac{4+2 \sqrt{3}-\sqrt{2}-\sqrt{6}}{1+\sqrt{3}-\sqrt{2}}$.
如图, $P$ 为正方形 $A B C D$ 对角线 $B D$ 上一动点, 若 $A B=2$, 则 $A P$ $+B P+C P$ 的最小值为

求所有的正整数 $x, y$ 满足方程 $\sqrt{x y+2019}=\sqrt{x}+\sqrt{2019}$.
我们需要从 25 匹马中挑选出最快的 3 匹马. 我们没有计时器, 但 我们有一个可以同时让 5 匹马赛跑的跑道, 然后我们可以比较这 5 匹 马的速度. 假设每匹马都以匀速奔跑, 并且所有马的速度不相等. 证 明: 你可以在 7 次赛马中挑选出最快的 3 匹马, 并确定这 3 匹马的速 度快慢顺序.
$\triangle A B C$ 的三边边长都是整数, $D, E$ 是 $B C$ 边上的相异两 点, 使得 $B, D, E, C$ 依次排列. 若 $B D=4, E C=7$, 且存在一个过 $D, E$ 的圆与 $A B, A C$ 都相切, 求 $\triangle A B C$ 周长可能的最小值.
已知 $a=\sqrt[3]{4}+\sqrt[3]{2}+\sqrt[3]{1}$, 那么 $\frac{3}{a}+\frac{3}{a^2}+\frac{3}{a^3}=$