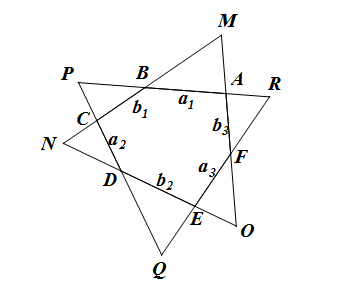
如图, $\triangle M N O$ 和 $\triangle P Q R$ 是两个全等的等边三角形. 六边形 $A B C D E F$ 的边长分别记为
$$
\begin{aligned}
& A B=a_1, B C=b_1, C D=a_2, \\
& D E=b_2, E F=a_3, F A=b_3 .
\end{aligned}
$$
求证: $a_1^2+a_2^2+a_3^2=b_1^2+b_2^2+b_3^2$.
$$
\begin{aligned}
& A B=a_1, B C=b_1, C D=a_2, \\
& D E=b_2, E F=a_3, F A=b_3 .
\end{aligned}
$$
求证: $a_1^2+a_2^2+a_3^2=b_1^2+b_2^2+b_3^2$.
