单选题 (共 10 题 ),每题只有一个选项正确
8 的相反数是
$\text{A.}$ -8
$\text{B.}$ $-\frac{1}{8}$
$\text{C.}$ $\frac{1}{8}$
$\text{D.}$ 8
反比例函数 $y=-\frac{4}{x}$ 的图象一定经过的点是
$\text{A.}$ $(1,4)$
$\text{B.}$ $(-1,-4)$
$\text{C.}$ $(-2,2)$
$\text{D.}$ $(2,2)$
若两个相似三角形周长的比为 $1: 4$, 则这两个三角形对应边的比是
$\text{A.}$ 1:2
$\text{B.}$ 1:4
$\text{C.}$ 1: 8
$\text{D.}$ 1: 16
如图, $A B / / C D, A D \perp A C$, 若 $\angle 1=55^{\circ}$, 则 $\angle 2$ 的度数为

$\text{A.}$ $35^{\circ}$
$\text{B.}$ $45^{\circ}$
$\text{C.}$ $50^{\circ}$
$\text{D.}$ $55^{\circ}$
估计 $\sqrt{2}(\sqrt{8}+\sqrt{10})$ 的值应在
$\text{A.}$ 7 和 8 之间
$\text{B.}$ 8 和 9 之间
$\text{C.}$ 9 和 10 之间
$\text{D.}$ 10 和 11 之间
用长度相同的木根按如图所示的规律拼图案, 其中第(1)个图案用了 9 根木棍, 第(2)个图案用了 14 根木根, 第 (3)个图案用了 19 根木根, 第(4)个图案用了 24 根木棍, …按此规律排列下去, 则第(8)个图案用的木棍根数是

$\text{A.}$ 39
$\text{B.}$ 44
$\text{C.}$ 49
$\text{D.}$ 54
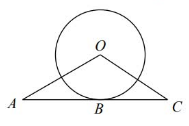
如图, $A C$ 是 $\odot O$ 的切线, $B$ 为切点, 连接 $O A, O C$. 若 $\angle A=30^{\circ}, A B=2 \sqrt{3}, B C=3$, 则 $O C$ 的长度是
$\text{A.}$ 3
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ $\sqrt{13}$
$\text{D.}$ 6
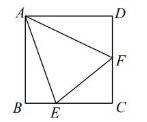
如图, 在正方形 $A B C D$ 中, 点 $E, F$ 分别在 $B C, C D$ 上, 连接 $A E, A F, E F, \angle E A F=45^{\circ}$. 若 $\angle B A E=\alpha$, 则 $\angle F E C$ 一定等于
$\text{A.}$ $2 \alpha$
$\text{B.}$ $90^{\circ}-2 \alpha$
$\text{C.}$ $45^{\circ}-\alpha$
$\text{D.}$ $90^{\circ}-\alpha$
在多项式 $x-y-z-m-n$ (其中 $x>y>z>m>n$ ) 中, 对相邻的两个字母间任意添加绝对值符号, 添加 绝对值符号后仍只有减法运算, 然后进行去绝对值运算, 称此为 “绝对操作”.
例如: $x-y-|z-m|-n=x-y-z+m-n,|x-y|-z-|m-n|=x-y-z-m+n, \cdots$. 下列说法:
(1)存在 “绝对操作”, 使其运算结果与原多项式相等;
(2)不存在“绝对操作”, 使其运算结果与原多项式之和为 0 ;
(3)所有的 “绝对操作” 共有 7 种不同运算结果.
其中正确的个数是
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
填空题 (共 8 题 ),请把答案直接填写在答题纸上
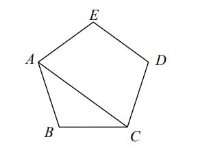
如图, 正五边形 $A B C D E$ 中, 连接 $A C$, 那么 $\angle B A C$ 的度数为
一个口袋中有 1 个红色球, 有 1 个白色球, 有 1 个蓝色球, 这些球除颜色外都相同. 从中随机摸出一个球, 记 下颜色后放回, 摇匀后再从中随机摸出一个球, 则两次都摸到红球的概率是
某新建工业园区今年六月份提供就业岗位 1501 个, 并按计划逐月增长, 预计八月份将提供岗位 1815 个. 设 七、八两个月提供就业岗位数量的月平均增长率为 $x$, 根据题意, 可列方程为
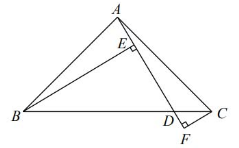
如图, 在 Rt $\triangle A B C$ 中, $\angle B A C=90^{\circ}, A B=A C$, 点 $D$ 为 $B C$ 上一点, 连接 $A D$. 过点 $B$ 作 $B E \perp A D$ 于点 $E$, 过点 $C$ 作 $C F \perp A D$ 交 $A D$ 的延长线于点 $F$, 若 $B E=4, C F=1$, 则 $E F$ 的长度为
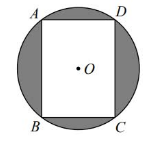
如图, $\odot O$ 是矩形 $A B C D$ 的外接圆, 若 $A B=4, A D=3$, 则图中阴影部分的面积为 (结果保留 $\pi$ )
若关于 $x$ 的一元一次不等式组 $\left\{\begin{array}{l}\frac{x+3}{2} \leqslant 4, \\ 2 x-a \geqslant 2\end{array}\right.$ 至少有 2 个整数解, 且. 关于 $y$ 的分式方程 $\frac{a-1}{y-2}+\frac{4}{2-y}=2$ 有非负整数解, 则所有满足条件的整数 $a$ 的值之和是
如果一个四位自然数 $\overline{a b c d}$ 的各数位上的数字互不相等且均不为 0 , 满足 $\overline{a b}-\overline{b c}=\overline{c d}$, 那么称这个四位数 为 “递减数”. 例如: 四位数 $4129, \because 41-12=29, \therefore 4129$ 是 “递减数”; 又如: 四位数 $5324, \because 53-32=21 \neq$ $24, \therefore 5324$ 不是 “递减数”. 若一个“递减数”为 $\overline{a 312}$, 则这个数为 4312 ; 若一个 “递减数” 的前三个数字组 成的三位数 $\overline{a b c}$ 与后三个数字组成的三位数 $\overline{b c d}$ 的和能被 9 整除, 则满足条件的数的最大值是
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算:
(1) $a(2-a)+(a+1)(a-1)$;
(2) $\frac{x^2}{x^2+2 x+1} \div\left(x-\frac{x}{x+1}\right)$.
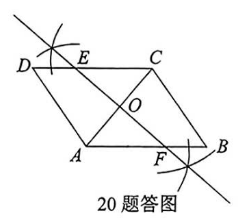
学习了平行四边形后, 小虹进行了拓展性研究. 她发现, 如果作平行四边形一条对角线的垂直平分线, 那么 这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分. 她的解决思路是通过证明对应线段所 在的两个三角形全等得出结论. 请根据她的思路完成以下作图与填空:
用直尺和圆规, 作 $A C$ 的垂直平分线交 $D C$ 于点 $E$, 交 $A B$ 于点 $F$, 垂足为点 $O$. (只保留作图痕迹)
已知: 如图, 四边形 $A B C D$ 是平行四边形, $A C$ 是对角线, $E F$ 垂直平分 $A C$, 垂足为点 $O$. 求证: $O E=O F$. 证明: $\because$ 四边形 $A B C D$ 是平行四边形,
$$
\begin{aligned}
& \therefore D C / / A B . \\
& \therefore \angle E C O=(1)
\end{aligned}
$$
$$
\begin{aligned}
& \because E F \text { 垂直平分 } A C, \\
& \therefore(2) \\
& \text { 又 } \angle E O C=\text { (3) } \\
& \therefore \triangle C O E \cong \triangle A O F(A S A) . \\
& \therefore O E=O F .
\end{aligned}
$$
小虹再进一步研究发现,过平行四边形对角线 $A C$ 中点的直线与平行四边形一组对边相交形成的线段均有 此特征. 请你依照题意完成下面命题:
过平行四边形对角线中点的直线 (4)
为了解 $A 、 B$ 两款品质相近的智能玩具飞机在一次充满电后运行的最长时间, 有关人员分别随机调查了 $A$ 、 $B$ 两款智能玩具飞机各 10 架, 记录下它们运行的最长时间 (分钟), 并对数据进行整理、描述和分析 (运行最 长时间用 $x$ 表示, 共分为三组:合格 $60 \leqslant x < 70$, 中等 $70 \leqslant x < 80$, 优等 $x \geqslant 80$, 下面给出了部分信息:
$A$ 款智能玩具飞机 10 架一次充满电后运行最长时间是:
$$
60,64,67,69,71,71,72,72,72,82 \text {. }
$$
$B$ 款智能玩具飞机 10 架一次充满电后运行最长时间属于中等的数据是:
$$
70,71,72,72,73
$$

根据以上信息, 解答下列问题:
(1) 上述图表中 $a=, b=, m=$
(2) 根据以上数据, 你认为哪款智能玩具飞机运行性能更好? 请说明理由 (写出一条理由即可);
(3) 若某玩具仓库有 $A$ 款智能玩具飞机 200 架、 $B$ 款智能玩具飞机 120 架, 估计两款智能玩具飞机运行性能 在中等及以上的共有多少架?
某公司不定期为员工购买某预制食品厂生产的杂酱面、牛肉面两种食品.
(1) 该公司花费 3000 元一次性购买了杂酱面、牛肉面共 170 份, 此时杂酱面、牛肉面的价格分别为 15 元、 20 元, 求购买两种食品各多少份?
(2) 由于公司员工人数和食品价格有所调整, 现该公司分别花费 1260 元、 1200 元一次性购买杂酱面、牛肉面 两种食品, 已知购买杂酱面的份数比牛肉面的份数多 $50 \%$, 每份杂酱面比每份牛肉面的价格少 6 元, 求购买 牛肉面多少份?
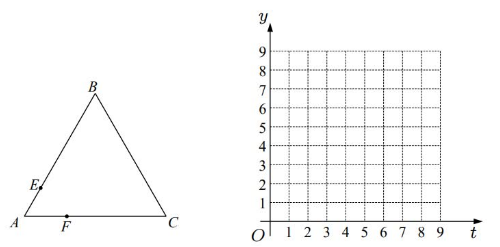
如图, $\triangle A B C$ 是边长为 4 的等边三角形, 动点 $E, F$ 分别以每秒 1 个单位长度的速度同时从点 $A$ 出发, 点 $E$ 沿折线 $A \rightarrow B \rightarrow C$ 方向运动, 点 $F$ 沿折线 $A \rightarrow C \rightarrow B$ 方向运动, 当两者相遇时停止运动. 设运动时间为 $t$ 秒, 点 $E, F$ 的距离为 $y$.
(1) 请直接写出 $y$ 关于 $t$ 的函数表达式并注明自变量 $t$ 的取值范围;
(2) 在给定的平面直角坐标系中画出这个函数的图象, 并写出该函数的一条性质;
(3) 结合函数图象, 写出点 $E, F$ 相距 3 个单位长度时 $t$ 的值.
为了满足市民的需求, 我市在一条小河 $A B$ 两侧开辟了两条长跑锻炼线路, 如图:
(1) $A-D-C-B$; (2) $A-E-B$. 经勘测, 点 $B$ 在点 $A$ 的正东方, 点 $C$ 在点 $B$ 的正北方 10 千米处, 点 $D$ 在 点 $C$ 的正西方 14 千米处, 点 $D$ 在点 $A$ 的北偏东 $45^{\circ}$ 方向, 点 $E$ 在点 $A$ 的正南方, 点 $E$ 在点 $B$ 的南偏西 $60^{\circ}$ 方
向. (参考数据: $\sqrt{2} \approx 1.41, \sqrt{3} \approx 1.73)$
(1) 求 $A D$ 的长度. (结果精确到 1 千米)
(2) 由于时间原因, 小明决定选择一条较短线路进行锻炼, 请计算说明他应该选择线路(1)还是线路(2)?

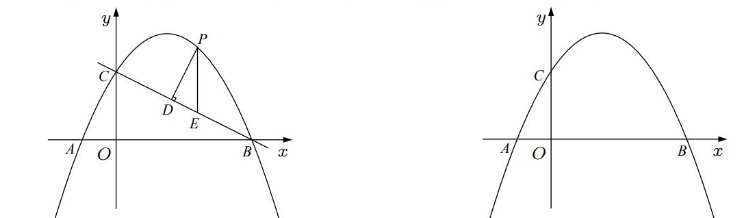
如图, 在平面直角坐标系中, 抛物线 $y=a x^2+b x+2$ 过点 $(1,3)$, 且交 $x$ 轴于点 $A(-1,0), B$ 两点, 交 $y$ 轴于点 $C$.
(1) 求抛物线的表达式;
(2) 点 $P$ 是直线 $B C$ 上方抛物线上的一动点, 过点 $P$ 作 $P D \perp B C$ 于点 $D$, 过点 $P$ 作 $y$ 轴的平行线交直线 $B C$ 于点 $E$, 求 $\triangle P D E$ 周长的最大值及此时点 $P$ 的坐标;
(3) 在 (2) 中 $\triangle P D E$ 周长取得最大值的条件下, 将该抛物线沿射线 $C B$ 方向平移 $\sqrt{5}$ 个单位长度, 点 $M$ 为平 移后的抛物线的对称轴上一点. 在平面内确定一点 $N$, 使得以点 $A, P, M, N$ 为顶点的四边形是菱形, 写出 所有符合条件的点 $N$ 的坐标, 并写出求解点 $N$ 的坐标的其中一种情况的过程.
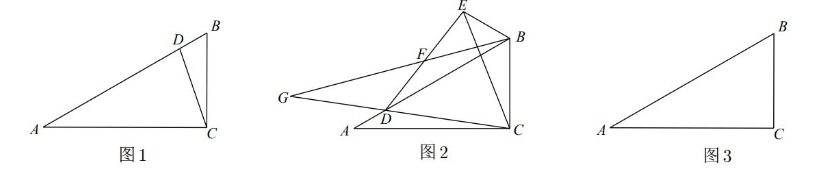
在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, \angle B=60^{\circ}$, 点 $D$ 为线段 $A B$ 上一动点, 连接 $C D$.
(1) 如图 1, 若 $A C=9, B D=\sqrt{3}$, 求线段 $A D$ 的长.
(2) 如图 2, 以 $C D$ 为边在 $C D$ 上方作等边 $\triangle C D E$, 点 $F$ 是 $D E$ 的中点, 连接 $B F$ 并延长, 交 $C D$ 的延长线于点
$G$. 若 $\angle G=\angle B C E$, 求证: $G F=B F+B E$.
(3) 在 $C D$ 取得最小值的条件下, 以 $C D$ 为边在 $C D$ 右侧作等边 $\triangle C D E$. 点 $M$ 为 $C D$ 所在直线上一点, 将 $\triangle B E M$ 沿 $B M$ 所在直线翻折至 $\triangle A B C$ 所在平面内得到 $\triangle B N M$. 连接 $A N$, 点 $P$ 为 $A N$ 的中点, 连接 $C P$, 当 $C P$ 取最大值时, 连接 $B P$, 将 $\triangle B C P$ 沿 $B C$ 所在直线翻折至 $\triangle A B C$ 所在平面内得到 $\triangle B C Q$, 请直接写出 此时 $\frac{N Q}{C P}$ 的值.