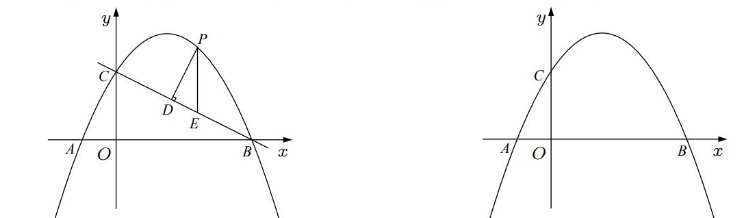
如图, 在平面直角坐标系中, 抛物线 $y=a x^2+b x+2$ 过点 $(1,3)$, 且交 $x$ 轴于点 $A(-1,0), B$ 两点, 交 $y$ 轴于点 $C$.
(1) 求抛物线的表达式;
(2) 点 $P$ 是直线 $B C$ 上方抛物线上的一动点, 过点 $P$ 作 $P D \perp B C$ 于点 $D$, 过点 $P$ 作 $y$ 轴的平行线交直线 $B C$ 于点 $E$, 求 $\triangle P D E$ 周长的最大值及此时点 $P$ 的坐标;
(3) 在 (2) 中 $\triangle P D E$ 周长取得最大值的条件下, 将该抛物线沿射线 $C B$ 方向平移 $\sqrt{5}$ 个单位长度, 点 $M$ 为平 移后的抛物线的对称轴上一点. 在平面内确定一点 $N$, 使得以点 $A, P, M, N$ 为顶点的四边形是菱形, 写出 所有符合条件的点 $N$ 的坐标, 并写出求解点 $N$ 的坐标的其中一种情况的过程.
(1) 求抛物线的表达式;
(2) 点 $P$ 是直线 $B C$ 上方抛物线上的一动点, 过点 $P$ 作 $P D \perp B C$ 于点 $D$, 过点 $P$ 作 $y$ 轴的平行线交直线 $B C$ 于点 $E$, 求 $\triangle P D E$ 周长的最大值及此时点 $P$ 的坐标;
(3) 在 (2) 中 $\triangle P D E$ 周长取得最大值的条件下, 将该抛物线沿射线 $C B$ 方向平移 $\sqrt{5}$ 个单位长度, 点 $M$ 为平 移后的抛物线的对称轴上一点. 在平面内确定一点 $N$, 使得以点 $A, P, M, N$ 为顶点的四边形是菱形, 写出 所有符合条件的点 $N$ 的坐标, 并写出求解点 $N$ 的坐标的其中一种情况的过程.
