学习了平行四边形后, 小虹进行了拓展性研究. 她发现, 如果作平行四边形一条对角线的垂直平分线, 那么 这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分. 她的解决思路是通过证明对应线段所 在的两个三角形全等得出结论. 请根据她的思路完成以下作图与填空:
用直尺和圆规, 作 $A C$ 的垂直平分线交 $D C$ 于点 $E$, 交 $A B$ 于点 $F$, 垂足为点 $O$. (只保留作图痕迹)
已知: 如图, 四边形 $A B C D$ 是平行四边形, $A C$ 是对角线, $E F$ 垂直平分 $A C$, 垂足为点 $O$. 求证: $O E=O F$. 证明: $\because$ 四边形 $A B C D$ 是平行四边形,
$$
\begin{aligned}
& \therefore D C / / A B . \\
& \therefore \angle E C O=(1)
\end{aligned}
$$
$$
\begin{aligned}
& \because E F \text { 垂直平分 } A C, \\
& \therefore(2) \\
& \text { 又 } \angle E O C=\text { (3) } \\
& \therefore \triangle C O E \cong \triangle A O F(A S A) . \\
& \therefore O E=O F .
\end{aligned}
$$
小虹再进一步研究发现,过平行四边形对角线 $A C$ 中点的直线与平行四边形一组对边相交形成的线段均有 此特征. 请你依照题意完成下面命题:
过平行四边形对角线中点的直线 (4)
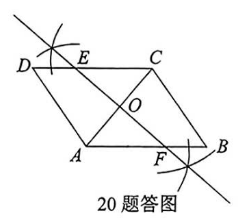
用直尺和圆规, 作 $A C$ 的垂直平分线交 $D C$ 于点 $E$, 交 $A B$ 于点 $F$, 垂足为点 $O$. (只保留作图痕迹)
已知: 如图, 四边形 $A B C D$ 是平行四边形, $A C$ 是对角线, $E F$ 垂直平分 $A C$, 垂足为点 $O$. 求证: $O E=O F$. 证明: $\because$ 四边形 $A B C D$ 是平行四边形,
$$
\begin{aligned}
& \therefore D C / / A B . \\
& \therefore \angle E C O=(1)
\end{aligned}
$$
$$
\begin{aligned}
& \because E F \text { 垂直平分 } A C, \\
& \therefore(2) \\
& \text { 又 } \angle E O C=\text { (3) } \\
& \therefore \triangle C O E \cong \triangle A O F(A S A) . \\
& \therefore O E=O F .
\end{aligned}
$$
小虹再进一步研究发现,过平行四边形对角线 $A C$ 中点的直线与平行四边形一组对边相交形成的线段均有 此特征. 请你依照题意完成下面命题:
过平行四边形对角线中点的直线 (4)
