单选题 (共 10 题 ),每题只有一个选项正确
$-\frac{1}{5}$ 的相反数是 ( )
$\text{A.}$ $5$
$\text{B.}$ $\frac{1}{5}$
$\text{C.}$ $-\frac{1}{5}$
$\text{D.}$ $-5$
如图, 面积为 1 的等边三角形 $A B C$ 中, $D, E, F$ 分别是 $A B, B C$, $C A$ 的中点, 则 $\triangle D E F$ 的面积是 ( )

$\text{A.}$ $1$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{4}$
下列给出的等边三角形、平行四边形、圆及扇形中,既是轴对称图形又是中心对称图形的是( )
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于 ( )

$\text{A.}$ 10
$\text{B.}$ 5
$\text{C.}$ 4
$\text{D.}$ 3
如图,数轴上两点M,N所对应的实数分别为m,n,则$m﹣n$的结果可能是( )
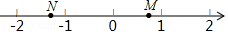
$\text{A.}$ -1
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
下列运算正确的是( )
$\text{A.}$ $3 a^{2}-a^{2}=3$
$\text{B.}$ $(a+b)^{2}=a^{2}+b^{2}$
$\text{C.}$ $\left(-3 a b^{2}\right)^{2}=-6 a^{2} b^{4}$
$\text{D.}$ $a \cdot a^{-1}=1(a \neq 0)$
我国古代著作《四元玉鉴》记载 “买椽多少” 问题: “六贯二百一十钱, 倩人去买几株椽. 每 株脚钱三文足, 无钱准与一株椽., 其大意为: 现请人代买一批椽, 这批椽的价钱为 6210 文. 如果每株椽的运费是 3 文, 那么少拿一株椽后, 剩下的椽的运费恰好等于一株椽的 价钱, 试问 6210 文能买多少株椽? 设这批椽的数量为 $x$ 株, 则符合题意的方程是 ( )
$\text{A.}$ $3(x-1)=\frac{6210}{x}$
$\text{B.}$ $\frac{6210}{x-1}=3$
$\text{C.}$ $3 x-1=\frac{6210}{x}$
$\text{D.}$ $\frac{6210}{x}=3$
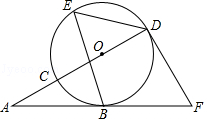
如图, 四边形 $A B C D$ 内接于 $\odot O, A B=C D, A$ 为 $\widehat{B D}$ 中点, $\angle B D C=60^{\circ}$, 则 $\angle A D B$ 等于 ( )

$\text{A.}$ $40^{\circ}$
$\text{B.}$ $50^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $70^{\circ}$
已知 $P_{1}\left(x_{1}, y_{1}\right), P_{2}\left(x_{2}, y_{2}\right)$ 是抛物线 $y=a x^{2}-2 a x$ 上的点, 下列命题正确的是 ( )
$\text{A.}$ 若 $\left|x_{1}-1\right|>\left|x_{2}-1\right|$, 则 $y_{1}>y_{2}$
$\text{B.}$ 若 $\left|x_{1}-1\right|>\left|x_{2}-1\right|$, 则 $y_{1} < y_{2}$
$\text{C.}$ 若 $\left|x_{1}-1\right|=\left|x_{2}-1\right|$, 则 $y_{1}=y_{2}$
$\text{D.}$ 若 $y_{1}=y_{2}$, 则 $x_{1}=x_{2}$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若从甲、乙、丙 3 位 “爱心辅学” 志愿者中随机选 1 位为学生在线辅导功课, 则甲被选到的
概率为
一个扇形的圆心角是 $90^{\circ}$, 半径为 4, 则这个扇形的面积为 ( ) . (结果保留 $\pi$ )
2020 年 6 月 9 日, 我国全海深自主遥控潜水器 “海斗一号” 在马里亚纳海沟刷新了我国潜 水器下潜深度的纪录, 最大下潜深度达 10907 米. 假设以马里亚纳海沟所在海域的海平 面为基准, 记为 0 米, 高于马里亚纳海沟所在海域的海平面 100 米的某地的高度记为 $+100$ 米, 根据题意, “海斗一号” 下潜至最大深度 10907 米处, 该处的高度可记为 ( ) 米.
如图所示的六边形花环是用六个全等的直角三角形拼成的, 则 $\angle A B C=$度.

设 $A, B, C, D$ 是反比例函数 $y=\frac{k}{x}$ 图象上的任意四点, 现有以下 结论:
(1)四边形 $A B C D$ 可以是平行四边形;
(2)四边形 $A B C D$ 可以是菱形;
(3)四边形 $A B C D$ 不可能是矩形;
(4)四边形 $A B C D$ 不可能是正方形.
其中正确的是 . (写出所有正确结论的序号)
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
解不等式组: $\left\{\begin{array}{l}2 x \leq 6-x, \text { ( } 1) \\ 3 x+1>2(x-1) .\end{array}\right.$
如图, 点 $E, F$ 分别在菱形 $A B C D$ 的边 $B C, C D$ 上, 且 $B E=D F$. 求证: $\angle B A E=\angle D A F$.

先化简, 再求值: $\left(1-\frac{1}{x+2}\right) \div \frac{x^{2}-1}{x+2}$, 其中 $x=\sqrt{2}+1$.
某公司经营甲、乙两种特产, 其中甲特产每吨成本价为 10 万元, 销售价为 $10.5$ 万元; 乙特 产每吨成本价为 1 万元, 销售价为 $1.2$ 万元. 由于受有关条件限制, 该公司每月这两种特 产的销售量之和都是 100 吨, 且田特产的销售量都不超过 20 吨.
(1)若该公司某月销售甲、乙两种特产的总成本为 235 万元, 问这个月该公司分别销售 甲、乙两种特产各多少吨?
(2)求该公司一个月销售这两种特产所能获得的最大总利润.
如图, $A B$ 与 $\odot O$ 相切于点 $B, A O$ 交 $\odot O$ 于点 $C, A O$ 的延长线交 $\odot O$ 于点 $D, E$ 是 $\widehat{B C D}$ 上不与 $B, D$ 重合的点, $\sin A=\frac{1}{2}$.
(1)求 $\angle B E D$ 的大小;
(2) 若 $\odot O$ 的半径为 3 , 点 $F$ 在 $A B$ 的延长线上, 且 $B F=3 \sqrt{3}$, 求证: $D F$ 与 $\odot O$ 相切.
为贯彻落实党中央关于全面建成小康社会的战略部署, 某贫困地区的广大党员干部深入农村
积极开展 “精准扶贫” 工作. 经过多年的精心帮扶, 截至 2019 年底, 按照农民人均年纯
收入 3218 元的脱贫标准, 该地区只剩少量家庭尚末脱贫. 现从这些尚末脱贫的家庭中随
机抽取 50 户, 统计其 2019 年的家庭人均年纯收入, 得到如图 1 所示的条形图.
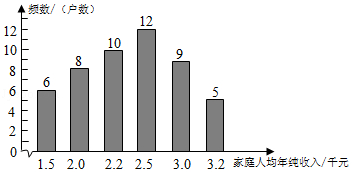
(1)如果该地区尚末脱贫的家庭共有 1000 户, 试估计其中家庭人均年纯收入低于 2000 元(不含 2000 元)的户数;
(2)估计 2019 年该地区尚末脱贫的家庭人均年纯收入的平均值;
(3) 2020 年初, 由于新冠疫情, 农民收入受到严重影响, 上半年当地农民家庭人均月纯 收入的最低值变化情况如图 2 的折线图所示. 为确保当地农民在 2020 年全面脱贫, 当地 政府积极筹集资金, 引进某科研机构的扶贫专项项目. 据预测, 随着该项目的实施, 当 地农民自 2020 年 6 月开始, 以后每月家庭人均月纯收入都将比上一个月增加 170 元.
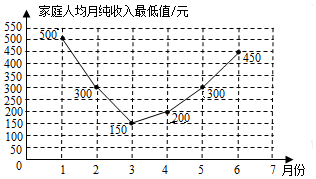
已知 2020 年农村脱贫标准为农民人均年纯收入 4000 元, 试根据以上信息预测该地区所 有贫困家庭能否在今年实现全面脱贫.
如图, $C$ 为线段 $A B$ 外一点.
(1)求作四边形 $A B C D$, 使得 $C D / / A B$, 且 $C D=2 A B$; (要求: 尺规作图, 不写作法, 保留作图痕迹)
(2) 在 (1) 的四边形 $A B C D$ 中, $A C, B D$ 相交于点 $P, A B, C D$ 的中点分别为 $M, N$, 求证: $M, P, N$ 三点在同一条直线上.

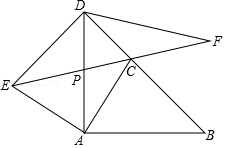
如图, $\triangle A D E$ 由 $\triangle A B C$ 绕点 $A$ 按逆时针方向旋转 $90^{\circ}$ 得到, 且点 $B$ 的对应点 $D$ 恰好落在
$B C$ 的延长线上, $A D, E C$ 相交于点 $P$.
(1) 求 $\angle B D E$ 的度数;
(2) $F$ 是 $E C$ 延长线上的点, 且 $\angle C D F=\angle D A C$.
(1)判断 $D F$ 和 $P F$ 的数量关系, 并证明;
(2)求证: $\frac{E P}{P F}=\frac{P C}{C F}$.
已知直线 $l_{1}: y=-2 x+10$ 交 $y$ 轴于点 $A$, 交 $x$ 轴于点 $B$, 二次函数的图象过 $A, B$ 两点, 交 $x$ 轴于另一点 $C, B C=4$, 且对于该二次函数图象上的任意两点 $P_{1}\left(x_{1}, y_{1}\right), P_{2}\left(x_{2}, y_{2}\right)$, 当 $x_{1}>x_{2} \geqslant 5$ 时, 总有 $y_{1}>y_{2}$.
(1)求二次函数的表达式;
(2) 若直线 $l_{2}: y=m x+n(n \neq 10)$, 求证:当 $m=-2$ 时, $l_{2} / / l_{1}$;
(3) $E$ 为线段 $B C$ 上不与端点重合的点, 直线 $l_{3}: y=-2 x+q$ 过点 $C$ 且交直线 $A E$ 于点 $F$, 求 $\triangle A B E$ 与 $\triangle C E F$ 面积之和的最小值.