单选题 (共 10 题 ),每题只有一个选项正确
$-\frac{1}{2023}$ 的相反数为
$\text{A.}$ $2023$
$\text{B.}$ $-2023$
$\text{C.}$ $\frac{1}{2023}$
$\text{D.}$ $-\frac{1}{2023}$
如图, $A O \perp B O$, 垂足为点 $O$, 直线 $C D$ 经过点 $O$. 若 $\angle 1=120^{\circ}$, 则 $\angle 3$ 的度数为
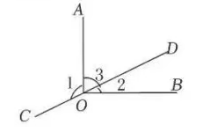
$\text{A.}$ $120^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $40^{\circ}$
$\text{D.}$ $30^{\circ}$
已知一个水分子的直径约为 $3.85 \times 10^{-9}$ 米. 某花粉的直径约为 $5 \times 10^{-4}$ 米, 用科学记数法表示一个水分子的直径是这种花粉直径的 ( ) 倍
$\text{A.}$ $0.77 \times 10^{-5}$ 倍
$\text{B.}$ $77 \times 10^{-4}$倍
$\text{C.}$ $7.7 \times 10^{-6}$倍
$\text{D.}$ $7.7 \times 10^{-5}$倍
下列计算结果正确的是
$\text{A.}$ $7 a-5 a=2$
$\text{B.}$ $9 a \div 3 a=3 a$
$\text{C.}$ $a^5 \div a^3=a^2$
$\text{D.}$ $\left(3 a^2\right)^3=9 a^6$
如图, 棱形 $A B C D$ 中, 对角线 $A C 、 B D$ 相交于点 $O, H$ 为 $A D$ 边中点, 棱形 $A B C D$ 的周长为 $20, B D=8$. 则 $\tan \angle H O D$ 的值等于
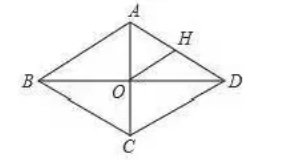
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{4}{3}$
若一元二次方程 $x^2-2 x+m=0$ 有两个不相同的实数根, 则实数 $m$ 的取值范围是
$\text{A.}$ $m \geqslant 1$
$\text{B.}$ $m \leqslant 1$
$\text{C.}$ $m > 1$
$\text{D.}$ $m < 1$
疾控中心每学期都对我校学生进行健康体检, 小亮将领航班所有学生测量体温的 结果制成如下统计图衣. 下列说法不正确的是

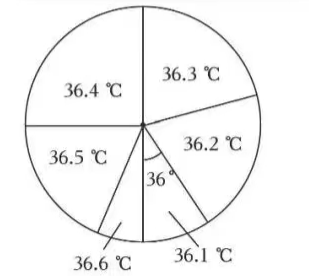
$\text{A.}$ 这个班有 40 名学生
$\text{B.}$ $m=8$
$\text{C.}$ 这些体温的众数是 8
$\text{D.}$ 这些体温的中位数是 36.35
如图, 在平面直角坐标系中, 已知点 $A(-3,0), B(0,4)$, 将 Rt $\triangle A B O$ 顺着 $x$ 轴无滑动的滚动. 第一次滚动到①的位置, 点 $A$ 的对应点记作点 $A_1$; 第二次滚动到② 的位置, 点 $A_1$ 的对应点记作点 $A_2$; 第三次滚动到③的位置, 点 $A_2$ 的对应点记作点 $A_3 ; \cdots$ 依次进行下去, 发地点 $A(-3,0), A_1(0,3), A_2(9,0), \cdots$, 则点 $A_{2023}$ 的坐标为

$\text{A.}$ $(8088,3)$
$\text{B.}$ $(8088,0)$
$\text{C.}$ $(8089,3)$
$\text{D.}$ $(8089,0)$
如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现,如图2是该台灯电流$I$与电阻$R$成反比例函数的图像,该图像经过点$P(880,0.25)$ 根据图像可知,下来说法正确的是
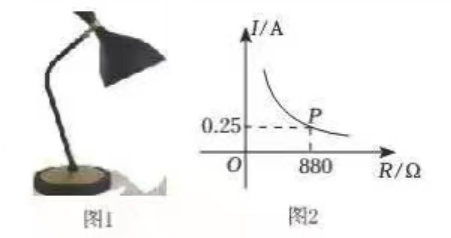
$\text{A.}$ 当 $R < 0.25$ 时, $I < 880$
$\text{B.}$ $I$ 与 $R$ 的函数关系式是 $I=\frac{200}{\mathrm{R}}(R>0)$
$\text{C.}$ 当 $R>1000$ 时, $I>0.22$
$\text{D.}$ 当 $880 < R < 1000$ 时, $I$ 的取值范因是 $0.22 < I < 0.25$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
已知正比例函数为 $y=m x^{|m+1|}$, 则 $m$ 的值为
已知关于 $x$ 的一元二次方程 $(k-2) x^2-2 x+1=0$. 从 $-4,-2,0,2,4$ 中任选一个数字作为 $k$ 代入原方程, 则选取的数字能令方程有实数根的概率为
如图, 在 $\triangle A B C$ 中, $\angle A B C=90^{\circ}$, 将 $\triangle A B C$ 沿 $A B$ 方向平移 $A D$ 的长度得到 $\triangle D F F$, 已知 $E F=8, B E=3, C G=3$. 则图中阴影部分的面积

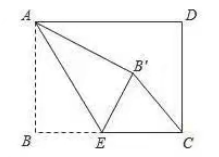
如图, 矩形 $A B C D$ 中, $A B=3, B C=4$, 点 $E$ 是 $B C$ 边上一点, 连接 $A E$, 把 $\angle B$ 沿 $A E$ 折叠,使点 $B$ 落在点 $B^{\prime}$ 处. 当 $\triangle C E B^{\prime}$ 为直角三角形时, $B E$ 的长为
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1) :计算 $(\pi+1)^0+2^{-2} -\frac{1}{2} \sin 30^{\circ}+|-\sqrt{9}|$;
(2) 化简: $\left(a+1-\frac{3}{a-1}\right) \div \frac{a^2+4 a+4}{a-1}$.
综合与实践
综合与实践课上, 老师与同学们以 “特殊的三角形” 为主题开展数学活动.
(1) 操作判断
如图 1, 在 $\triangle A B C$ 中, $\angle A B C=90^{\circ}, A B=B C$, 点 $P$ 是直线 $A C$ 上一动点.
操作:连接 $B P$, 将线段 $B P$ 绕点 $P$ 逆时针旋转 $90^{\circ}$ 得到 $P D$, 连接 $D C$, 如图 2 .
根据以上操作, 判断: 如图 3 , 当点 $P$ 与点 $A$ 重合时, 则四边形 $A B C D$ 的形状是
(2) 过移探究
①如㚵 4 , 当点 $P$ 与点 $C$ 重合时, 连接 $D B$, 判断四迄形 $A B D C$ 的形状, 并说明理由:
② 当点 $P$ 与点 $A$, 点 $C$ 都不重合时, 试猜想 $D C$ 与 $B C$ 的位置关系, 并利用图 2 让明你的猜想;
(3) 拓展应用
当点 $P$ 与点 $A$, 点 $C$ 都不重合时, 若 $A B=4, A P=3$, 请直接写出 $C D$ 的长.
