单选题 (共 8 题 ),每题只有一个选项正确
由题意可得 $A=\{x \mid x>2\}, B=\{y \mid y \geqslant 0\}$, 则 $A \cap B=\{x \mid x>2\}$.
$\text{A.}$ $\varnothing$
$\text{B.}$ $[4,+\infty)$
$\text{C.}$ $[2,+\infty)$
$\text{D.}$ $[0,2]$
已知抛物线 $C: x^2=2 p y(p>0)$ 的焦点为 $F$, 点 $C A(4,2)$ 在抛物线 $C$ 上, 则 $|A F|=$
$\text{A.}$ $4$
$\text{B.}$ $2 \sqrt{5}$
$\text{C.}$ $8$
$\text{D.}$ $4 \sqrt{5}$
已知 $a>2$, 则 $2 a+\frac{8}{a-2}$ 的最小值是
$\text{A.}$ 6
$\text{B.}$ 8
$\text{C.}$ 10
$\text{D.}$ 12
如图, 在四棱雉 $P-A B C D$ 中, 平面 $P A D \perp$ 平面 $A B C D$, 四边形 $A B C D$ 是矩形, $P A=P D=$ $\sqrt{2} A B, E, F$ 分别是棱 $B C, P D$ 的中点, 则异面直线 $E F$ 与 $A B$ 所成角的余弦值是

$\text{A.}$ $\frac{\sqrt{3}}{3}$
$\text{B.}$ $\frac{\sqrt{6}}{3}$
$\text{C.}$ $\frac{\sqrt{3}}{6}$
$\text{D.}$ $\frac{\sqrt{6}}{6}$
已知直线 $l_1:(a-1) x-(2 a+3) y+a+4=0$ 与圆 $C: x^2+y^2+2 x-m-2=0$, 则 “ $m>2$ ” 是 “直线 $l$ 与圆 $C$ 一定相交”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
溶液酸碱度是通过 $P H$ 计量的, $P H$ 的计算公式为 $P H=-\lg \left[H^{+}\right]$, 其中 $\left[H^{+}\right]$表示溶液中氢离子的浓度, 单位是摩尔/升. 已知某 溶液的 $P H$ 值为 2.921 , 则该溶液中氢离子的浓度约为 ( 取 $\lg 2=0.301, \lg 3=0.477)$
$\text{A.}$ $1.2 \times 10^{-3}$ 摩尔/升
$\text{B.}$ $1.2 \times 10^{-4}$ 摩尔/升
$\text{C.}$ $6 \times 10^{-3}$ 摩尔/升
$\text{D.}$ $6 \times 10^{-4}$ 摩尔/升
春节期间, 某地政府在该地的一个广场布置了一个如图所示的圆形花坛, 花坛分为 5 个区域. 现有 5 种不同 的花卉可供选择, 要求相邻区域不能布置相同的花卉, 且每个区域只布置一种花卉, 则不同的布置方案有
$\text{A.}$ 120种
$\text{B.}$ 240种
$\text{C.}$ 420种
$\text{D.}$ 720种
若函数 $f(x)=4 \cos (2 x+\varphi)-2 \sqrt{2}(0 \leq \varphi \leq \pi)$ 在 $\left[0, \frac{11 \pi}{6}\right]$ 内恰有 4 个零点, 则 $\varphi$ 的取值范围是
$\text{A.}$ $\left[0, \frac{\pi}{4}\right] \cup\left[\frac{\pi}{2}, \frac{7 \pi}{12}\right]$
$\text{B.}$ $\left[\frac{\pi}{12}, \frac{\pi}{4}\right] \cup\left[\frac{\pi}{2}, \frac{7 \pi}{12}\right]$
$\text{C.}$ $\left[0, \frac{\pi}{4}\right] \cup\left[\frac{7 \pi}{12}, \pi\right]$
$\text{D.}$ $\left[\frac{\pi}{12}, \frac{\pi}{4}\right] \cup\left[\frac{7 \pi}{12}, \pi\right]$
多选题 (共 4 题 ),每题有多个选项正确
下列关于非零复数 $z_1, z_2$ 的结论正确的是
$\text{A.}$ 若 $z_1, z_2$ 互为共轭复数, 则 $z_1 \cdot z_2 \in R$
$\text{B.}$ 若 $z_1 \cdot z_2 \in R$, 则 $z_1, z_2$ 互为共轭复数
$\text{C.}$ 若 $z_1, z_2$ 互为共轭复数, 则 $\left|\frac{z_1}{z_2}\right|=1$
$\text{D.}$ 若 $\left|\frac{z_1}{z_2}\right|=1$, 则 $z_1, z_2$ 互为共轭复数
已知 $x>0, y>0$, 且 $x-y>\ln \frac{y}{x}$, 则
$\text{A.}$ $x>y$
$\text{B.}$ $x+\frac{1}{y}>y+\frac{1}{x}$
$\text{C.}$ $\ln (x-y) < 0$
$\text{D.}$ $\frac{1}{2^x} < 2^{-y}$
若 $\triangle A B C$ 的三个内角均小于 $120^{\circ}$, 点 $M$ 满足 $\angle A M B=\angle A M C=\angle B M C=120^{\circ}$, 则点 $M$ 到三角形三个顶点的距离之和最小, 点 $M$ 被人们称为费马点. 根据以上性质, 已知 $\vec{a}$ 是平面内任意一个向量, 向量 $\vec{b}, \vec{c}$ 满足 $\vec{b} \perp \vec{c}$, 且 $|\vec{b}|=2|\vec{c}|=2 \sqrt{3}$, 则 $|\vec{a}-\vec{b}|+|\vec{a}-\vec{c}|+|\vec{a}+\vec{c}|$ 的取值可以是
$\text{A.}$ $9$
$\text{B.}$ $4 \sqrt{3}$
$\text{C.}$ $3 \sqrt{3}$
$\text{D.}$ $6$
已知 $f^{\prime}(x), g^{\prime}(x)$ 分别是定义在 $R$ 上的函数 $f(x), g(x)$ 的导函数, $f(x+1)-g(3-x)=3, f^{\prime}(x-2)=g^{\prime}(x+$ $2)$, 且 $f(x+1)$ 是奇函数, 则
$\text{A.}$ $g(x)$ 的图象关于直线 $x=4$ 对称
$\text{B.}$ $f(x)$ 的图象关于点 $(-1,0)$ 对称
$\text{C.}$ $\sum_{k=1}^{2025} f(k)=0$
$\text{D.}$ $\sum_{k=1}^{2025} g(k)=0$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
某蛋糕店新推出一款蛋糕, 连续一周每天的销量分别为 $18,22,25,29,21,20,19$, 则这组数据的平均数是
在等比数列 $\left\{a_n\right\}$ 中, 若 $a_1+a_3=62, a_2+a_4=31$, 则当 $a_1 a_2 \cdots a_n$ 取得最大值时, $n=$
一个正方体的体积为 $m$ 立方米, 表面积为 $n$ 平方米, 则 $m-n$ 的最小值是 ( ) , 此时, 该正方体内切球的体积是 ( ) 立方 米.
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的右焦点为 $F$, 直线 $l: y=\sqrt{3} x$ 与双曲线 $C$ 交于 $A, B$ 两点, 若 $A F \perp A B$, 则双曲线 $C$ 的离 心率是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n, a_1+a_5=10, S_7=49$.
(1) 求 $\left\{a_n\right\}$ 的通项公式;
(2) 若 $b_n=(-1)^{n+1} S_n$, 求数列 $\left\{b_n\right\}$ 的前 100 项和.
某校为了解高三年级学生的学习情况, 进行了一次高考模拟测试, 从参加测试的高三学生中随机抽取 200 名学生的成绩进行分 析, 得到如下列联表:
将频率视为概率.

(1)从该校高三男、女学生中各随机抽取 1 名, 求这 2 名高三学生中恰有 1 名的成绩在本科分数线以下的概率;
( 2 ) 从该校所有高三学生中随机抽取 3 名, 记被抽取到的 3 名高三学生本次高考模拟成绩在本科分数线以上 (包含本科分数线) 的男生人数为 $X$, 求 $X$ 的分布列和数学期望 $E(X)$.
在 $\triangle A B C$ 中, 内角 $A, B, C$ 所对的边分别是 $a, b, c$, 且 $\cos 2 A+\cos (B+C)=0$.
(1)求角 $A$ 的大小;
(2) 若 $\overrightarrow{B C}=3 \overrightarrow{B D}$, 且 $\triangle A B C$ 的面积是 $6 \sqrt{3}$, 求 $A D$ 的最小值.
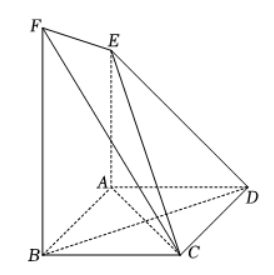
如图, 在多面体 $A B C D E F$ 中, 四边形 $A B C D$ 是菱形, $\angle A B C=60^{\circ}$, 平面 $A D E \perp$ 平面 $A B C D, A E$ $/ / B F, D E=\sqrt{2} A D=\sqrt{2} A E$.
(1) 证明: $B D \perp$ 平面 $A C E$ ;
(2) 若平面 $C E F$ 与平面 $A B F E$ 夹角的余弦值为 $\frac{\sqrt{10}}{4}$, 求 $B F$ 的长.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\frac{\sqrt{3}}{3}$, 点 $A\left(1, \frac{4 \sqrt{3}}{3}\right)$ 在椭圆 $C$ 上.
(1)求椭圆 $C$ 的标准方程;
( 2 ) 过点 $M(0,3)$ 的直线 $l$ 交椭圆 $C$ 于 $P, Q$ 两点, $O$ 为坐标原点, 求 $\triangle O P Q$ 面积的最大值.
已知函数 $f(x)=e^{2 x}+(a-2) e^x-a x$.
(1) 讨论 $f(x)$ 的单调性;
(2) 若 $f(x)$ 有两个零点, 求 $a$ 的取值范围.