单选题 （共 10 题 ），每题只有一个选项正确
下列图形中，是轴对称图形且对称轴条数最多的是
$\text{A.}$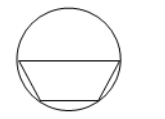 
$\text{B.}$ 
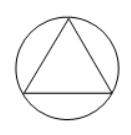$\text{C.}$ 
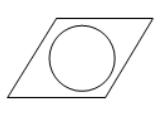$\text{D.}$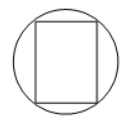 
如图所示，$\angle A=50^{\circ}, \angle B=20^{\circ}, \angle D=30^{\circ}$ ，则 $\angle B C D$ 的度数为
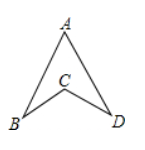
$\text{A.}$ $80^{\circ}$
$\text{B.}$ $100^{\circ}$
$\text{C.}$ $120^{\circ}$
$\text{D.}$ $140^{\circ}$
一个多边形的内角和是它的外角和的4倍．这个多边形是
$\text{A.}$ 六边形
$\text{B.}$ 九边形
$\text{C.}$ 八边形
$\text{D.}$ 十边形
如图，已知 $\angle A B C=\angle B A D$ ，再添加一个条件，仍不能判定 $\triangle A B C \cong \triangle B A D$ 的是
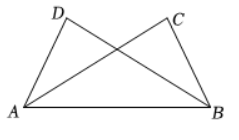
$\text{A.}$ $\angle A B D=\angle B A C$
$\text{B.}$ $\angle C=\angle D$
$\text{C.}$ $A D=B C$
$\text{D.}$ $A C=B D$
工人师傅常用角尺平分一个任意角，做法如下：如图，$\angle A O B$ 是一个任意角，在边 $O A 、 O B$ 上分别取 $O M=O N$ ，移动角尺，使角尺两边相同的刻度分别与点 $M 、 N$ 重合，过角尺顶点 $C$ 作射线 $O C$ ，由此作法便可得 $\triangle N O C \cong \triangle M O C$ ，其依据是
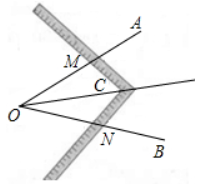
$\text{A.}$ SSS
$\text{B.}$ SAS
$\text{C.}$ ASA
$\text{D.}$ AAS
如图为二环四边形，它的内角和 $\angle A+\angle B+\angle C+\angle D+\angle A_1+\angle B_1+\angle C_1+\angle D_1$ 度数为
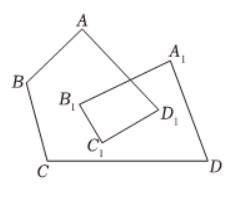
$\text{A.}$ $360^{\circ}$
$\text{B.}$ $540^{\circ}$
$\text{C.}$ $720^{\circ}$
$\text{D.}$ $900^{\circ}$
满足下列条件的三角形是等边三角形的个数是
（1）有两个角是 $60^{\circ}$ 的三角形
（2）有两个外角相等的等腰三角形
（3）腰上的高也是中线的等腰三角形
（4）三个外角都相等的三角形
（5）有一个角为 $60^{\circ}$ 的等腰三角形．
$\text{A.}$ 2 个
$\text{B.}$ 3 个
$\text{C.}$ 4 个
$\text{D.}$ 5 个
如图，$\triangle A B C$ 中边 $A B$ 的垂直平分线分别交 $B C, A B$ 于点 $D, E, A E=3 \mathrm{~cm}, \triangle A D C$ 的周长为 9 cm ，则 $\triangle A B C$ 的周长是
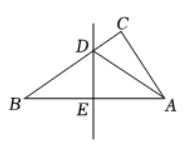
$\text{A.}$ 10 cm
$\text{B.}$ 12 cm
$\text{C.}$ 15 cm
$\text{D.}$ 17 cm
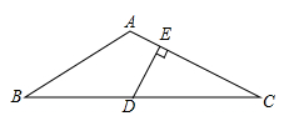
如图，$\triangle A B C$ 中，$B E$ 是角平分线，$D E \| B C$ 交 $A B$ 于 $D$ ，交 $A C$ 于 $E$ ，若 $D E=8, A D=5$ ，则 $A B$ 等于
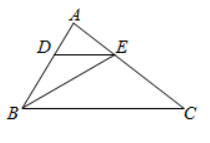
$\text{A.}$ 12
$\text{B.}$ 13
$\text{C.}$ 14
$\text{D.}$ 15
如图，在平面直角坐标系中，对 $\triangle A B C$ 令进行循环往复的轴对称变换，若原来点 $A$ 坐标 $(1,2)$ ，则经过第 2023 次变换后点 $A$ 的对应点的坐标为
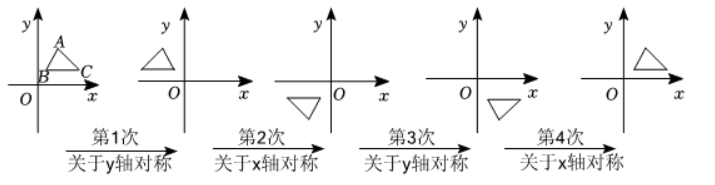
$\text{A.}$ $(1,-2)$
$\text{B.}$ $(-1,-2)$
$\text{C.}$ $(-1,2)$
$\text{D.}$ $(1,2)$
填空题 （共 5 题 ），请把答案直接填写在答题纸上
计算：
（1）$-a^2 \cdot a^3=$ $\_\_\_\_$ ；
（2）$x^m \cdot x \cdot x^{n-2}=$ $\_\_\_\_$ ．
已知实数 $x, y$ 满足 $|x-3|+\sqrt{y-7}=0$ ，则以 $x, y$ 的值为两边长的等腰三角形的周长是
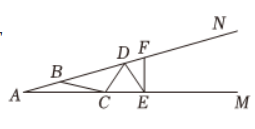
如图，若 $B, D, F$ 在 $A N$ 上，$C, E$ 在 $A M$ 上，且 $A B=B C=C D=E D=E F, \angle A=20^{\circ}$ ，则 $\angle F E M=$
如图，在 $R t \triangle A B C$ 中，$\angle B=90^{\circ}$ ，以顶点 $C$ 为圆心，适当长为半径画弧，分别交 $A C, B C$ 于点 $E, F$ ，再分别以点 $E, F$ 为圆心，大于 $\frac{1}{2} E F$ 的长为半径画弧，两弧交于点 $P$ ，作射线 $C P$ 交 $A B$ 于点 $D$ ．若 $B D=3, A C=1$ 0 ，则 $\triangle A C D$ 的面积是
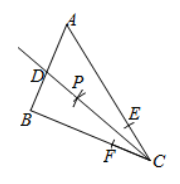
如图，在 $\triangle A B C$ 中，$A B=A C, S_{\triangle A B C}=12, B C=3$ ，点 $D$ 为边 $B C$ 的中点，$A C$ 的垂直平分线 $E F$ 分别交边 $A B, A C$ 于点 $E, F$ ．点 $P$ 为线段 $E F$ 上一动点，则 $\triangle P C D$ 周长的最小值为
解答题 （共 8 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
计算：
（1） $2 x^2 y \cdot\left(-2 x y^2\right)^3+(2 x y)^3 \cdot\left(-x y^2\right)^2$ ；
（2）$(2 a+3 b)(a-b)-(3 a-2 b)(a+b)$ ．
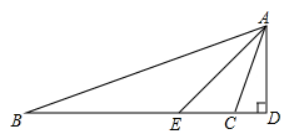
在 $\triangle A B C$ 中，$\angle B=20^{\circ}, \angle A C B=110^{\circ}, A E$ 平分 $\angle B A C, A D \perp B D$ 于点 $D$ ，求 $\angle E A D$ 的度数．
如图，已知：在 $\triangle A F D$ 和 $\triangle C E B$ 中，点 $A 、 E 、 F 、 C$ 在同一直线上，$A E=C F, \angle B=\angle D, A D \| B C$ ．求证：$A D=B C$ ．
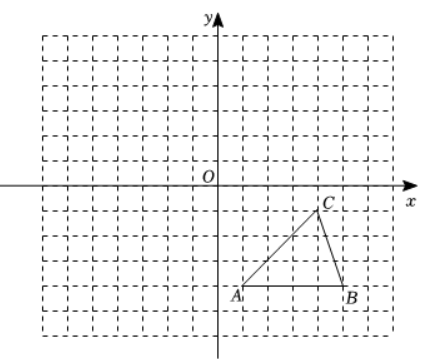
已知：方格纸中的每个小方格都是边长为 1 个单位的正方形，在建立平面直角坐标系后，$\triangle A B C$ 的顶点均在格点上，点 $C$ 的坐标为 $(4,-$ 1）。
（1）请以 $y$ 轴为对称轴，画出与 $\triangle A B C$ 对称的 $\triangle A_1 B_1 C_1$ ，并直接写出点 $A_1$ 、 $B_1 、 C_1$ 的坐标；
（2）$\triangle A B C$ 的面积是 $\_\_\_\_$ ；
（3）点 $P(a+1, b-1)$ 与点 $C$ 关于 $x$ 轴对称，则 $a=$ $\_\_\_\_$ ，$b=$ $\_\_\_\_$。
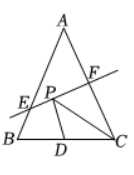
如图，$\triangle A B C$ 中，$A B=A C, \angle B A C=120^{\circ}, D$ 为 $B C$ 的中点，$D E \perp A C$ 于 $E, A E=1$ ，求 $C E$ 的长．
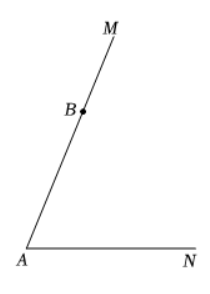
如图，已知 $\triangle M A N$ ，点 $B$ 在射线 $A M$ 上．
（1）尺规作图，在 $A N$ 上取一点 $C$ ，使 $B C=B A$ ，作 $\angle M B C$ 的平分线 $B D$ ．（保留作图痕迹，不可作法）
（2）在（1）的条件下，求证：$B D \| A N$ ．
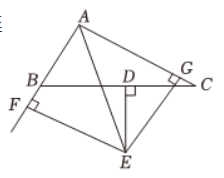
如图，已知 $\triangle A B C$ 中 $B C$ 边的垂直平分线 $D E$ 与 $\angle B A C$ 的平分线交于点 $E, E F \perp A B$ 交 $A B$ 的延长线于点 $F, B G \perp A C$ 交 $A C$ 于点 $G$ ．
（1）求证：$B F=C G$ ；
（2）若 $A B=12, A C=16$ ，求 $A F$ 的长度．
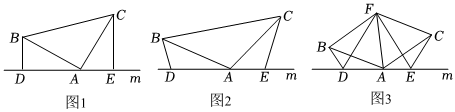
（1）如图（1），已知：在 $\triangle A B C$ 中，$\angle B A C=90^{\circ}, A B=A C$ ，直线 $m$ 经过点 $A, B D \perp$ 直线 $m, C E \perp$ 直线 $m$ ，垂足分别为点 $D 、 E$ ，则 $B D 、 D E 、 C E$ 的数量关系为 $\_\_\_\_$ ．
（2）如图（2），将（1）中的条件改为：在 $\triangle A B C$ 中，$A B=A C, D 、 A 、 E$ 三点都在直线 $m$ 上，并且有 $\angle B D A=\angle A E C=\angle B A C =\alpha$ ，其中 $\alpha$ 为任意锐角或钝角．请问（1）中结论是否成立？如成立，请你给出证明；若不成立，请说明理由．
（3）如图（3），$D 、 E$ 是 $D 、 A 、 E$ 三点所在直线 $m$ 上的两动点（ $D 、 A 、 E$ 三点互不重合）点 $F$ 为 $\angle B A C$ 平分线上的一点，且 $\triangle A B F$ 和 $\triangle A C F$ 均为等边三角形，连接 $B D 、 C E$ ，若 $\angle B D A=\angle A E C=\angle B A C$ ，求 $\angle D F E$ 的度数．
