单选题 (共 6 题 ),每题只有一个选项正确
设 $\alpha 、 \beta$ 是空间两个不同平面,$a 、 b 、 c$ 是空间三条不同直线,下列命题为真命题的是( )
$\text{A.}$ 若 $\alpha / / \beta, b / / \alpha$ ,则 $b / / \beta$
$\text{B.}$ 若直线 $a$ 与 $b$ 相交,$a / / \alpha, b / / \beta$ ,则 $\alpha$ 与 $\beta$ 相交
$\text{C.}$ 若 $\alpha \perp \beta, a / / \alpha$ ,则 $a \perp \beta$
$\text{D.}$ 若 $\alpha \perp \beta, \alpha \cap \beta=a, b \subset \alpha, b \perp a, c \perp \beta$ ,则 $b / / c$
在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中,$P$ 为 $B_1 D_1$ 的中点,则直线 $P B$ 与 $A D_1$ 成的角为
$\text{A.}$ $\frac{\pi}{2}$
$\text{B.}$ $\frac{\pi}{3}$
$\text{C.}$ $\frac{\pi}{4}$
$\text{D.}$ $\frac{\pi}{6}$
已知圆锥的高为 $\sqrt{6}$ ,其侧面展开图为一个半圆,则该圆锥的母线长为( )
$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ $2 \sqrt{6}$
$\text{D.}$ $4 \sqrt{2}$
已知圆柱的轴截面为正方形,其外接球为球 $O$ ,则圆柱的表面积与球 $O$ 的表面积之比为( )
$\text{A.}$ $3: 4$
$\text{B.}$ $1: 2$
$\text{C.}$ $3 \sqrt{2}: 8$
$\text{D.}$ 不能确定
攒尖是古代中国建筑中屋顶的一种结构形式,宋代称为撮尖,清代称攒尖.攒尖建筑的屋面在顶部交汇为一点,形成尖顶,依其平面有圆形攒尖、三角损尖、四角攒尖、八角攒尖。也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.辽宁省实验中学校园内的明心亭,为一个八角攒尖,它的主要部分的轮廓可近似看作一个正八棱锥,设正八棱锥的侧面等腰三角形的顶角为 $2 \theta$ ,它的侧棱与底面内切圆半径的长度之比为
$\text{A.}$ $\frac{\sqrt{2}-1}{\sin \theta}$
$\text{B.}$ $\frac{\sqrt{2}-1}{\cos \theta}$
$\text{C.}$ $\frac{1}{\sqrt{2} \sin \theta}$
$\text{D.}$ $\frac{1}{\sqrt{2} \cos \theta}$
如图,该几何体是由正方体截去八个一样的四面体得到的,若被截的正方体棱长为 2 ,则该几何体的表面积为
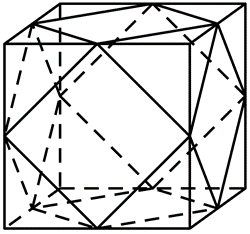
$\text{A.}$ $12+3 \sqrt{3}$
$\text{B.}$ $12+4 \sqrt{3}$
$\text{C.}$ $6+3 \sqrt{3}$
$\text{D.}$ $6+4 \sqrt{3}$
多选题 (共 3 题 ),每题有多个选项正确
设 $\alpha, \beta$ 为两个平面,下列是"$\alpha / / \beta$"的充分条件是( )
$\text{A.}$ $\alpha, \beta$ 与平面 $\gamma$ 都垂直
$\text{B.}$ $\alpha$ 内有两条相交直线与平面 $\beta$ 均无交点
$\text{C.}$ 异面直线 $a, b$ 满足 $a / / \alpha, b / / \beta$
$\text{D.}$ $\alpha$ 内有 5 个点(任意三点不共线)到 $\beta$ 的距离相等
如图,$M, N$ 为正方体中所在棱的中点,过 $M, N$ 两点作正方体的截面,则截面的形状可能为

$\text{A.}$ 三角形
$\text{B.}$ 四边形
$\text{C.}$ 五边形
$\text{D.}$ 六边形
如图,在四棱锥 $P-A B C D$ 中,底面 $A B C D$ 为直角梯形,$\angle A B C=\angle B A D=\frac{\pi}{2}, A P=A D=2 B C=2 A B, P A \perp$ 底面 $A B C D, M$ 为 $P A$ 的中点,则下列叙述中正确的是( )
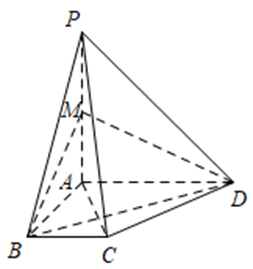
$\text{A.}$ $P C / /$ 平面 $M B D$
$\text{B.}$ $B D \perp$ 平面 $P A C$
$\text{C.}$ 异面直线 $B C$ 与 $P D$ 所成的角是 $\frac{\pi}{4}$
$\text{D.}$ 直线 $P C$ 与底面 $A B C D$ 所成的角的正切值是 $\sqrt{2}$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
已知一个圆台的上、下底面半径之比为 $1: 2$ ,母线长为 $2 \sqrt{2}$ ,其母线与底面所成的角为 $45^{\circ}$ ,则这个圆台的体积为 $\qquad$
若四棱锥 $P-A B C D$ 的各顶点都在同一个球 $O$ 的表面上,$P B \perp$ 底面 $A B C D, P B=2, A B=C D=1$ , $A D=2 B C=2 \sqrt{2}, B C / / A D$ ,则球 $O$ 的体积为
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
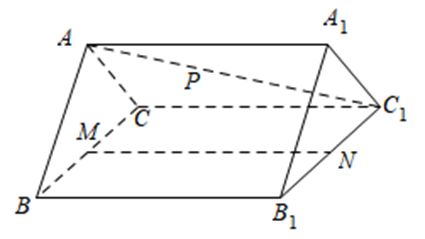
如图,在三棱柱 $A B C-A_1 B_1 C_1$ 中,平面 $A_1 A B B_1 \perp$ 平面 $A B C, A B \perp B C, B_1 B=A B=A B_1=4, B C=3$ , $D$ 为 $A C$ 的中点.
(1)求证:$A B_1 / /$ 平面 $B C_1 D$ ;
(2)求三棱锥 $B_1-A_1 C B$ 体积.
在三棱锥 $P-A B C$ 中,$A C=2, B C=4, \triangle P A C$ 为正三角形,$D$ 为 $A B$ 的中点,$A C \perp P D, \angle P C B=90^{\circ}$ .
(1)求证:$B C \perp$ 平面 $P A C$
(2)求 $P D$ 与平面 $P B C$ 所成角的正弦值.
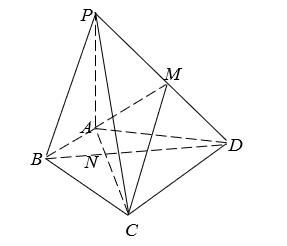
如图,在四棱锥 $P-A B C D$ 中,$P A \perp$ 平面 $A B C D, A C, B D$ 相交于点 $N, D N=2 N B$ ,已知 $P A=A C=A D=3$ , $B D=3 \sqrt{3}, \angle A D B=30^{\circ}$ .
(1)求证:$A C \perp$ 平面 $P A D$ ;
(2)设棱 $P D$ 的中点为 $M$ ,求平面 $P A B$ 与平面 $M A C$ 所成二面角的正弦值
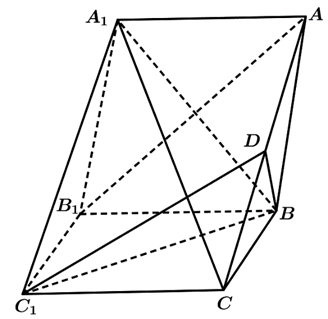
如图,在三棱柱 $A B C-A_1 B_1 C_1$ 中,$\triangle A B C$ 是边长为 2 的等边三角形,$B C \perp B B_1, C C_1=\sqrt{2}, A C_1=\sqrt{6}$ .
(1)证明:平面 $A B C \perp$ 平面 $B B_1 C_1 C$ ;
(2)$M, N$ 分别是 $B C, B_1 C_1$ 的中点,$P$ 是线段 $A C_1$ 上的动点,若二面角 $P-M N-C$ 的平面角的大小为 $30^{\circ}$ ,试确定点 $P$ 的位置.