单选题 (共 8 题 ),每题只有一个选项正确
$(1+5 i ) i$ 的虚部为
$\text{A.}$ $-1$
$\text{B.}$ $0$
$\text{C.}$ $1$
$\text{D.}$ $6$
设全集 $U=\{1,2,3,4,5,6,7,8,9\}$ ,集合 $A=\{1,3,5\}$ ,则 $\complement_U A$ 中元素个数为
$\text{A.}$ 0
$\text{B.}$ 3
$\text{C.}$ 5
$\text{D.}$ 8
若双曲线 $C$ 的虚轴长为实轴长的 7 倍,则 $C$ 的离心率为
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ 2
$\text{C.}$ $\sqrt{7}$
$\text{D.}$ $2 \sqrt{2}$
若点 $(a, 0)(a>0)$ 是函数 $y=2 \tan \left(x-\frac{\pi}{3}\right)$ 的图象的一个对称中心,则 $a$ 的最小值为
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $90^{\circ}$
$\text{D.}$ $135^{\circ}$
设 $f(x)$ 是定义在 $R$ 上且周期为 2 的偶函数,当 $2 \leqslant x \leqslant 3$ 时,$f(x)=5-2 x$ ,则 $f\left(-\frac{3}{4}\right)=$
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $-\frac{1}{4}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{1}{2}$
帆船比赛中,运动员可借助风力计测定风速的大小和方向,测出的结果在航海学中称为视风风速,视风风速对应的向量,是真风风速对应的向量与船行风速对应的向量之和,其中船行风速对应的向量与船速对应的向量大小相等,方向相反。图1给出了部分风力等级、名称与风速大小的对应关系。已知某帆船运动员在某时刻测得的视风风速对应的向量与船速对应的向量如图2(风速的大小和向量的大小相同,单位 $m / s$ ),则真风为
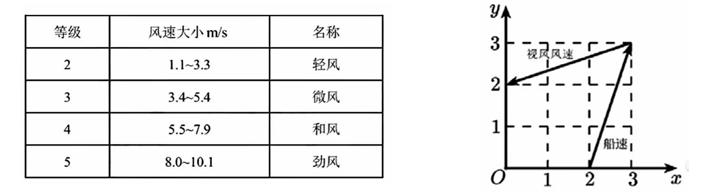
$\text{A.}$ 轻风
$\text{B.}$ 微风
$\text{C.}$ 和风
$\text{D.}$ 劲风
若圆 $x^2+(y+2)^2=r^2(r>0)$ 上到直线 $y=\sqrt{3} x+2$ 的距离为 $1$ 的点有且仅有 $2$ 个,则 $r$ 的取值范围是
$\text{A.}$ $(0,1)$
$\text{B.}$ $(1,3)$
$\text{C.}$ $(3,+\infty)$
$\text{D.}$ $(0,+\infty)$
若实数 $x, y, z_{\text {满足 }} 2+\log _2 x=3+\log _3 y=5+\log _5 z$ ,则 $x, y, z$ 的大小关系不可能是
$\text{A.}$ $x>y>z$
$\text{B.}$ $x>z>y$
$\text{C.}$ $y>x>z$
$\text{D.}$ $y>z>x$
多选题 (共 3 题 ),每题有多个选项正确
在正三棱柱 $A B C-A_1 B_1 C_1$ 中,$D$ 为 $B C$ 中点,则 ()
$\text{A.}$ $A D \perp A_1 C$
$\text{B.}$ $B C \perp$ 平面 $A A_1 D$
$\text{C.}$ $C C_1 / /$ 平面 $A A_1 D$
$\text{D.}$ $A D / / A_1 B_1$
设抛物线 $C: y^2=6 x$ 的焦点为 $F$ ,过 $F$ 的直线交 $C$ 于 $A 、 B$ ,过 $F$ 且垂直于 $A B$ 的直线交 $1: y=-\frac{3}{2} x$ 于 $E$ ,过 $A$ 作 $x=-\frac{3}{2}$ 的垂线,垂足为 $D$ ,则
$\text{A.}$ $|A D|=|A F|$
$\text{B.}$ $|A E|=|A B|$
$\text{C.}$ $|A B| \geq 6$
$\text{D.}$ $|A E| \cdot|B E| \geq 18$
已知 $\triangle A B C$ 的面积为 $\frac{1}{4}$ ,若 $\cos 2 A+\cos 2 B+2 \sin C=2, \cos A \cos B \sin C=\frac{1}{4}$ ,则( )
$\text{A.}$ $\sin C=\sin ^2 A+\sin ^2 B$
$\text{B.}$ $A B=\sqrt{2}$
$\text{C.}$ $\sin A+\sin B=\frac{\sqrt{6}}{2}$
$\text{D.}$ $A C^2+B C^2=3$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
若直线 $y=2 x+5$ 是曲线 $y= e ^x+x+a$ 的切线,则 $a=$
若一个等比数列的前 4 项和为 4 ,前 8 项和为 68 ,则该等比数列的公比为
在 1 个箱子里有 5 个球,分别以 $1 \sim 5$ 标号,若有放回取三次,记至少取出一次的球的个数 $X$ ,则 $E(X)=$ $\qquad$ .
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
为研究某疾病与超声波检查结果的关系,从做过超声波检查的人群中随机调查了 1000 人,得到如下列表:
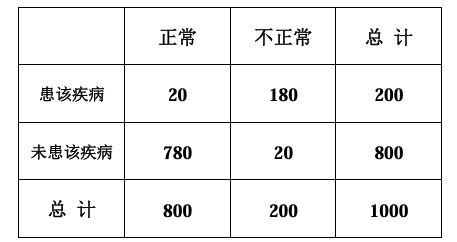
(1)记超声波结果检查不正常者患该疾病的概率为 $P$ ,求 $P$ 的估计值
(2)根据小概率值 $\alpha=0.001$ 的独立性检验,分析超声波检查的结果与是否患该疾病有关.

设数列 $\left\{a_n\right\}$ 满足 $a_1=3, \frac{a_{n+1}}{n}=\frac{a_n}{n+1}+\frac{1}{n(n+1)}$ .
(1)证明:$\left\{n a_n\right\}$ 为等差数列;
(2)设 $f(x)=a_1 x+a_2 x^2+\cdots+a_m x^m$ ,求 $f^{\prime}(-2)$ .
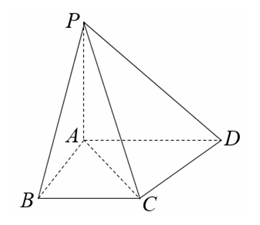
如图所示的四棱锥 $P-A B C D$ 中,$P A \perp$ 平面 $A B C D, B C / / A D, A B \perp A D$ .
(1)证明:平面 $P A B \perp P A D$ ;
(2)若 $P A=A B=\sqrt{2}, A D=\sqrt{3}+1, B C=2, P 、 B 、 C 、 D$ 在同一个球面上,设该球面的球心为 $O$ .
(i)证明:$O$ 在平面 $A B C D$ 上;
(ii)求直线 $A C$ 与直线 $P O$ 所成角的余弦值.
设椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ ,记 $A$ 为椭圆下端点,$B$ 为右端点,$|A B|=\sqrt{10}$ ,且椭圆 $C$ 的离心率为 $\frac{2 \sqrt{2}}{3}$ .
(1)求椭圆 $C$ 的标准方程;
(2)若 $P(m, n)$ 为平面内不在 $y$ 轴上一点,$R$ 是射线 $A P$ 上一点,且有 $|A P| \cdot|A R|=3$ .
(i)用 $m, n$ 表示 $R$ 的坐标;
(ii)设直线 $O R$ 的斜率为 $k_1$ ,直线 $O P$ 的斜率为 $k_2$ ,若 $k_1=3 k_2, Q$ 为 $C$ 上一点,求 $|P Q|$ 的最大值.
设函数 $f(x)=5 \cos x-\cos 5 x$ .
(1)求 $f(x)$ 在 $\left[0, \frac{\pi}{4}\right]$ 的最大值;
(2)给定 $\theta \in(0, \pi), a$ 为给定实数,证明:存在 $y \in[a-\theta, a+\theta]$ ,使得 $\cos y \leqslant \cos \theta$ ;
(3)若存在 $\varphi$ ,使得对任意 $x$ ,都有 $5 \cos x-\cos (5 x+\varphi) \leqslant b$ ,求 $b$ 的最小值.