单选题 （共 8 题 ），每题只有一个选项正确
集合 $\{x \in N \mid x+1 \leq 2\}$ 的另一种表示为 ( )
$\text{A.}$ $\{0,1,2,3\}$
$\text{B.}$ $\{0,1,2\}$
$\text{C.}$ $\{0,1\}$
$\text{D.}$ $\{1,2\}$
命题 " $\exists x>1, x^2-2 x+3>0$ " 的否定形式为 ( )
$\text{A.}$ $\exists x \leq 1, x^2-2 x+3 \leq 0$
$\text{B.}$ $\exists x>1, x^2-2 x+3 \leq 0$
$\text{C.}$ $\forall x \leq 1, x^2-2 x+3 \leq 0$
$\text{D.}$ $\forall x>1, x^2-2 x+3 \leq 0$
" $a>0$ 且 $b>0$ " 是 " $a b>0$ " 的 ( )
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知函数 $f(x+1)=2 x$, 则 $f(1)=(\quad)$
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
已知函数 $y=f(x)$ 的定义域是 $[-2,2]$ ，函数 $g(x)=\frac{f(x-1)}{x}$ ，则函数 $y=g(x)$ 的定义域是（）
$\text{A.}$ $[-1,3]$
$\text{B.}$ $[-1,0) \cup(0,3]$
$\text{C.}$ $[1,3]$
$\text{D.}$ $[-3,0) \cup(0,1]$
在同一直角坐标系中, 函数 $y=x^2+2 a x+a-1$ 与 $y=a^x(a>0$ 且 $a \neq 1)$ 的图象可能是
$\text{A.}$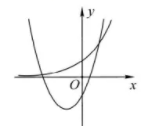 
$\text{B.}$ 
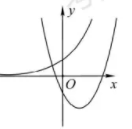$\text{C.}$ 
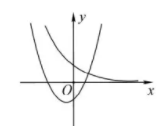$\text{D.}$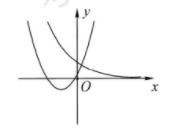 
已知函数 $f(x)$ 是定义在 $R$ 上的偶函数, 满足 $f(1)=0$, 且 $f(x)$ 在 $(0,+\infty)$ 上单调递减, 则不等式 $x f(x) < 0$ 的解集为 ( )
$\text{A.}$ $(-\infty,-1) \cup(1,+\infty)$
$\text{B.}$ $(-1,1)$
$\text{C.}$ $(-\infty,-1) \cup(0,1)$
$\text{D.}$ $(-1,0) \cup(1,+\infty)$
已知函数 $f(x)=\left\{\begin{array}{ll}(2 a-1)^x, & x < 0 \\ -x^2+(4 a-3) x+3 a-1, & x \geq 0\end{array}\right.$, 满 足 对 任 意 $x_1 \neq x_2$ 都 有 $\left(x_1-x_2\right)\left[f\left(x_1\right)-f\left(x_2\right)\right] < 0$ 成立, 则实数 $a$ 的取值范围是
$\text{A.}$ $\left(\frac{1}{2}, 1\right)$
$\text{B.}$ $\left(\frac{1}{2}, \frac{2}{3}\right]$
$\text{C.}$ $\left[\frac{2}{3}, \frac{3}{4}\right]$
$\text{D.}$ $\left(\frac{1}{2}, \frac{3}{4}\right]$
多选题 （共 3 题 ），每题有多个选项正确
下列命题为真命题的是（）
$\text{A.}$ 若 $a>b>0$, 则 $a c^2>b c^2$
$\text{B.}$ 若 $a>b>0$, 则 $\frac{b}{a} < \frac{b+1}{a+1}$
$\text{C.}$ 若 $a>b$, 则 $2^{-a} < 2^{-b}$
$\text{D.}$ 若 $a>b$, 则 $\frac{1}{a} < \frac{1}{b}$
下列说法正确的是
$\text{A.}$ 函数 $f(x)=1$ 与 $g(x)=x^0$ 是同一函数
$\text{B.}$ 函数 $f(x)=\frac{3}{x+2}(x \in[-1,1])$ 的值域为 $[1,3]$
$\text{C.}$ 设集合 $M=\{x \mid x>0\}, N=\{y \mid y \in R\}$ ，则对应关系 $f: x \rightarrow y^2=2 x$ 是集合 $M$ 到集合 $N$的函数
$\text{D.}$ 已知 $f(x)$ 是 $R$ 上的奇函数, 当 $x \geq 0$ 时, $f(x)=x^2-3 x$, 则 $x < 0$ 时 $f(x)=-x^2-3 x$
已知 $a, b$ 为正实数, 且 $a b+a+b=8$, 下列正确的是 ( )
$\text{A.}$ $a+b$ 的最小值为 4
$\text{B.}$ $a b$ 的最大值为 2
$\text{C.}$ $2 a+b$ 的最小值为 $6 \sqrt{2}-3$
$\text{D.}$ $\frac{1}{a+1}+\frac{1}{b+1}$ 的最小值为 $\frac{2}{3}$
填空题 （共 3 题 ），请把答案直接填写在答题纸上
已知幂函数 $y=f(x)$ 的图象过点 $(3, \sqrt{3})$, 则该函数的解析式为
关于 $x$ 的不等式 $x^2+a x+b < 0$ 的解集为 $\{x \mid-3 < x < 1\}$, 则关于 $x$ 的不等式 $x^2+b x+a < 0$ 的解集为
对于函数 $f(x)$, 若在定义域内存在实数 $x$, 满足 $f(-x)=-f(x)$, 则称 $f(x)$ 为 "弱原点对称函数". 已知函数 $g(x)=\left\{\begin{array}{ll}\left(2^x\right)^2-2 m \cdot 2^x-2, & -1 \leq x < 0 \\ 1, & 0 < x \leq 1\end{array}\right.$ 是定义域内的 "弱原点对称函数", 则实数 $m$ 的取值范围是
解答题 （共 5 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
(1) 化简求值: $(0.008)^{\frac{1}{3}}-\left(\frac{49}{4}\right)^{\frac{1}{2}}+(2 \sqrt{2})^{\frac{2}{3}}-5^{-1}+\pi^0$.
(2) 已知 $a^{\frac{1}{4}}+a^{-\frac{1}{2}}=4$, 求 $a^2+a^{-2}$ 的值.
已知集合 $A=\left\{x \mid x^2-3 x+2>0\right\}, B=\{x \mid 2 m-3 < x < m+2\}$.
(1) 当 $m=2$ 时, 求 $A \cup B$;
(2) 若 $\left(C_R A\right) \cap B=\phi$, 求 $m$ 的取值范围.
已知定义域为 $(-2,2)$ 的函数 $f(x)=\frac{a \cdot 3^x+b}{3^x+1}$ 是奇函数, 且 $f(1)=\frac{1}{2}$.
(1) 求出 $a, b$ 的值, 判断函数 $f(x)$ 在 $(-2,2)$ 上的单调性, 并用定义证明;
(2) 若 $f(m+1)+f(2 m-1) < 0$, 求实数 $m$ 的取值范围.
国家提出乡村振兴，建设新农村战略，鼓励农村产业发展. 某企业响应国家号召，在农村某地投资生产某种大型农机产品，其每日生产的总成本 $y$ （万元）与日产量 $x$ (件) 之间的函数关系可近似地表示为 $y=\frac{1}{2} x^2+b x+8(1 \leq x \leq 10)$, 且当 $x=10$ 时, $y=38$.
(1) 求 $b$ 的值;
(2) 计算该企业日产量 $x$ 为多少件时, 每日生产的平均成本 $\frac{y}{x}$ 最低?
(3) 国家实行惠农政策, 每件产品的售价定为 2 万元, 为了使企业可持续发展, 政府有两种补贴方案供企业选择. 方案一：根据日产量，每件产品补贴 1 万元；方案二：每日定额补贴 3 万元. 假设每天生产的产品都能销售完, 请你计算:
(1)如果选择方案一, 日产量 $x$ 为多少件时, 日利润最大（利润=销售额+补贴-总成本）？
(2)若日产量为 5 件时, 你认为选择哪种方案比较好?
已知函数 $h(x)=x+\frac{a}{x} \quad(a>0)$ 在区间 $(0, \sqrt{a})$ 上单调递减, 在区间 $(\sqrt{a},+\infty)$ 上单调递增, 现有函数 $f(x)=x+\frac{2}{x}$ 和函数 $g(x)=m x^2-(m-1) x+1$.
(1) 若 $x \in[1,2]$, 求函数 $f(x)$ 的最值;
(2) 若关于 $x$ 的不等式 $g(x) < 3$ 的解集为 $R$, 求实数 $m$ 的取值范围;
(3) 若对于 $\forall x_1 \in[4,6], \exists x_2 \in[1,2]$, 使得 $g\left(x_1\right) \leq f\left(x_2\right)+1$ 成立, 求实数 $m$ 的取值范围.