填空题 (共 8 题 ),请把答案直接填写在答题纸上
设 $A, B$ 是两个随机事件,已知
$$
P(A)=0.4, P(B)=0.3, P(A \cup B)=0.5
$$
则 $P(A \mid B)=$
三人独立地破译一个密码,他们能译出的概率分别是 $\frac{1}{5}, \frac{1}{3}, \frac{1}{4}$ ,则他们将此密码译出的概率 $p=$
已知随机变量 $X$ 的概率函数为
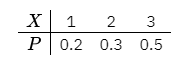
则 $F ( 2 . 7 )=$
设随机变量 $X \sim P(1), Y \sim e(1)$, 即 $f(y)=\left\{\begin{array}{cc}e^{-y}, & y>0, \\ 0, & y \leq 0 ;\end{array}\right.$ 且相关系数 $R(X, Y)=-\frac{1}{2}$ ,
则 $E(X+Y)=$ $\qquad$ ; $D(X+Y)=$
若随机变量 $X$ 服从 $N(0,4)$ ,则 $P(|X| < 2)=$
设随机变量 $X \sim t(n)$ ,则 $Y=X^2 \sim$
设 $X_1, X_2, X_3, X_4$ 为来自正态总体 $X \sim N\left(\mu, \sigma^2\right)$ 的样本,已知 $\hat{\mu}_1=\theta\left(X_1+2 X_2+X_3-X_4\right)$ ,
$$
\hat{\mu}_2=\frac{1}{4}\left(X_1+X_2+X_3+X_4\right)
$$
是总体均值 $\mu$ 的无偏估计量,则 $\theta=$ $\qquad$ ;且 $\hat{\mu}_1, \hat{\mu}_2$ 中较为有效的是 $\qquad$ (填 $\hat{\mu}_1$ 或 $\hat{\mu}_2$ ).
设随机变量 $(X, Y)$ 具有分布函数
$$
F(x, y)=\left\{\begin{array}{cc}
\left(1-e^{-x}\right)\left(1-e^{-y}\right), & x>0, y>0 ; \\
0, & \text { 其他; }
\end{array}\right.
$$
则 $X$ 的边缘概率密度 $f(x)=$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知随机变量 $X$ 的概率密度为
$$
f(x)=a e^{-|x|},-\infty < x < +\infty .
$$
求 (1) 参数 $a$ 的值; (2) 概率 $P(X>1)$ ; (3) 数学期望 $E(X)$.
某保险公司多年的资料表明,在索赔户中被盗索赔户占 $20 \%$ ,用 $X$ 表示在随意抽查的 100 个索赔户中因被盗向保险公司索赔的户数。
(1)写出 $X$ 的概率函数;
(2)利用棣莫佛-拉普拉斯中心极限定理,求索赔户中被盗索赔户不少于 14 户且不多于 30 户的概率 $P\{14 \leq X \leq 3 0 \}$ 的近似值.
设 $X \sim U(0,1)$, 求 $Y=e^X$ 的概率密度.
设连续总体 $X$ 的概率密度函数为
$$
f(x ; \theta)=\left\{\begin{array}{cc}
\theta x^{\theta-1}, & 0 < x < 1 \\
0, & \text { 其它 }
\end{array}(\theta>0),\right.
$$
$X_1, X_2, \cdots, X_n$ 为来自总体 $X$ 的样本,求未知参数 $\theta$ 的最大似然估计量.
从一批钉子中抽取 16 枚,测得长度的样本均值 $\bar{X}=2.125$ ,样本标准差为 $S=0.017$ ,设钉长分布为正态, $\sigma$ 为未知,试求总体期望 $\mu$ 的置信度为 0.90 的置信区间.
从一批轴料中取 15 件测量其椭圆度,已知椭圆度服从正态分布,计算得 $S=0.25$ ,问该批轴料椭圆度的总体方差与规定的 $\sigma^2=0.04$ 有无显著差别?
(取 $\alpha=0.05$ ).