单选题 （共 8 题 ），每题只有一个选项正确
$\dfrac{1}{6}$的相反数是（ ）
$\text{A.}$ $\dfrac{1}{6}$
$\text{B.}$ $-6$
$\text{C.}$ $6$
$\text{D.}$ $-\dfrac{1}{6}$
下列运算正确的是（ ）
$\text{A.}$ $m+2m＝3m^2$
$\text{B.}$ $2m^3 • 3m^2＝6m^6$
$\text{C.}$ $(2m)^3＝8m^3$
$\text{D.}$ $m^6÷m^2＝m^3$
已知一个正多边形的一个外角为 $36^{\circ}$, 则这个正多边形的边数是 （ ）
$\text{A.}$ 7
$\text{B.}$ 8
$\text{C.}$ 9
$\text{D.}$ 10
甲、乙、丙、丁四位同学五次数学测验成绩统计如下表所示，如果从这四位同学中，选出一位同学参加数学竞赛．那么应选 去 （ ）
$\text{A.}$ 甲
$\text{B.}$ 乙
$\text{C.}$ 丙
$\text{D.}$ 丁
下列几何体是由4个相同的小正方体搭成的，其中，主视图、左视图、俯视图都相同的是（ ）
$\text{A.}$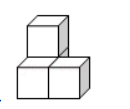 
$\text{B.}$ 
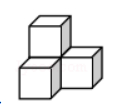$\text{C.}$ 
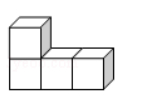$\text{D.}$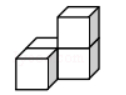 
在平面直角坐标系中，若点$A(a,-b)$在第三象限，则点$B(-ab,b)$所在的象限是（ ）
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
若菱形的周长为16，高为2，则菱形两邻角的度数之比为（ ）
$\text{A.}$ 4:1
$\text{B.}$ 5:1
$\text{C.}$ 6:1
$\text{D.}$ 7:1
2020年初以来，红星消毒液公司生产的消毒液在库存量为m吨的情况下，日销售量与产量持平．自1月底抗击“新冠病毒”以来，消毒液需求量猛增，该厂在生产能力不变的情况下，消毒液一度脱销，下面表示2020年初至脱销期间，该厂库存量y（吨）与时间t（天）之间函数关系的大致图象是（ ）
$\text{A.}$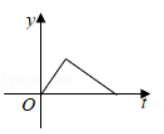 
$\text{B.}$ 
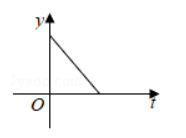$\text{C.}$ 
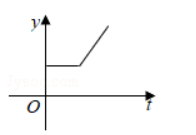$\text{D.}$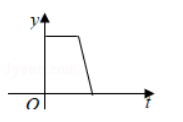 
填空题 （共 8 题 ），请把答案直接填写在答题纸上
已知 $x_{1}, x_{2}$ 是一元二次方程 $x^{2}-2 x-1=0$ 的两根, 则 $\frac{1}{x_{1} x_{2}}=$ （ ）
若 $|x-2|+\sqrt{x+y}=0$, 则 $-\frac{1}{2} x y=$ （ ）
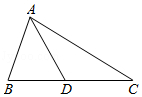
如图, 在 $\triangle A B C$ 中, 点 $D$ 在边 $B C$ 上, $A B=A D=D C, \angle C=35^{\circ}$, 则 $\angle B A D=$ （ ） 度
计算: $\frac{y}{x^{2}-y^{2}} \div\left(1-\frac{x}{x+y}\right)$ 的结果是 （ ）
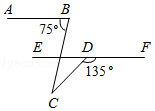
已知: 如图, $A B / / E F, \angle A B C=75^{\circ}, \angle C D F=135^{\circ}$, 则 $\angle B C D=$ （ ） 度.
我国古代数学著作《九章算术》中有这样一个问题：”今有池方一丈，葭（jiā）生其中央，出水一尺．引葭赴岸，适与岸齐．问水深几何？”（注：丈，尺是长度单位，1丈＝10尺）这段话翻译成现代汉语，即为：如图，有一个水池，水面是一个边长为1丈的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，则水池里水的深度是 （ ） 尺．
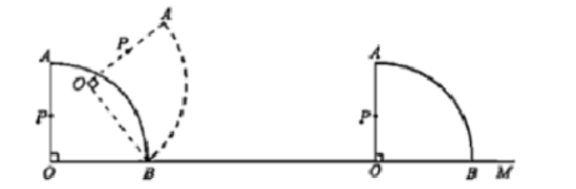
如图所示，将一个半径 $OA=10cm$，圆心角$ \angle AOB=90^\circ $ 的扇形纸板放置在水平面的一条射线OM上，在没有滑动的情况下，将扇形AOB沿射线OM翻转至OB，再次回到OM上时，则半径OA的中点P运动的路线长为（ ） cm（计算结果不取近似值）
解答题 （共 9 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
解不等式 $\frac{2}{3} x+\frac{1}{2} \geq \frac{1}{2} x$, 并在数轴上表示其解集.
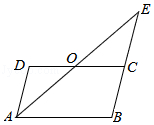
已知: 如图, 在 $\square A B C D$ 中, 点 $O$ 是 $C D$ 的中点, 连接 $A O$ 并延长, 交 $B C$ 的延长线于 点 $E$, 求证: $A D=C E$.
为推广黄冈各县市名优农产品，市政府组织创办了“黄冈地标馆”，一顾客在“黄冈地标馆”发现，如果购买6盒羊角春牌绿茶和4盒九孔牌藕粉，共需960元，如果购买1盒羊角春牌绿茶和3盒九孔牌藕粉共需300元，请问每盒羊角春牌绿茶和每盒九孔牌藕粉分别需要多少元？
为了解疫情期间学生网络学习的学习效果，东坡中学随机抽取了部分学生进行调查．要求每位学生从“优秀”，“良好”，“一般”，“不合格”四个等次中，选择一项作为自我评价网络学习的效果．现将调查结果绘制成如图两幅不完整的统计图，请结合图中所给的信息解答下列问题：
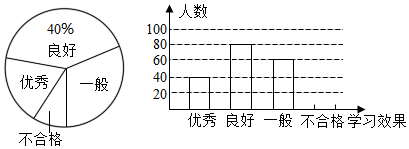
（1）这次活动共抽查了 （ ） 人．
（2）将条形统计图补充完整，并计算出扇形统计图中，学习效果“一般”的学生人数所在扇形的圆心角度数．
（3）张老师在班上随机抽取了4名学生，其中学习效果“优秀”的1人，“良好”的2人，“一般”的1人，若再从这4人中随机抽取2人，请用画树状图法，求出抽取的2人学习效果全是“良好”的概率．
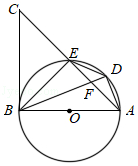
已知: 如图, $A B$ 是 $\odot O$ 的直径, 点 $E$ 为 $\odot O$ 上一点, 点 $D$ 是 $\widehat{A E}$ 上一点, 连接 $A E$ 并延 长至点 $C$, 使 $\angle C B E=\angle B D E, B D$ 与 $A E$ 交于点 $F$.
(1) 求证: $B C$ 是 $\odot O$ 的切线;
(2)若 $B D$ 平分 $\angle A B E$, 求证: $A D^{2}=D F \cdot D B$.
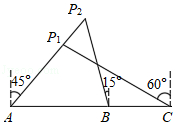
因东坡文化远近闻名的遗爱湖公园，“国庆黄金周”期间，游人络绎不绝，现有一艘游船载着游客在遗爱湖中游览，当船在A处时，船上游客发现岸上P1处的临摹亭和P2处的遗爱亭都在东北方向，当游船向正东方向行驶600m到达B处时，游客发现遗爱亭在北偏西15°方向，当游船继续向正东方向行驶400m到达C处时，游客发现临摹亭在北偏西60°方向．
（1）求A处到临摹亭P1处的距离；
（2）求临摹亭P1处于遗爱亭P2处之间的距离．（计算结果保留根号）
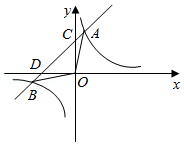
已知: 如图, 一次函数的图象与反比例函数的图象交于 $A, B$ 两点, 与 $y$ 轴正半轴交于点 $C$, 与 $x$ 轴负半轴交于点 $D, O B=\sqrt{5}, \tan \angle D O B=\frac{1}{2}$.
（1）求反比例函数的解析式;
（2） 当 $S_{\triangle A C O}=\frac{1}{2} S_{\triangle O C D}$ 时, 求点 $C$ 的坐标.
网络销售已经成为一种热门的销售方式, 为了减少农产品的库存, 我市市长亲自在某网络平台上进行直播销售大别山牌板栗, 为提高大家购买的积极性, 直播时, 板栗公司每天拿出 2000 元现金, 作为红包发给购头者. 已知该板栗的成本价格 为 6 元 $/ \mathrm{kg}$, 每日销售量 $y(\mathrm{~kg})$ 与销售单价 $x$ (元 $/ \mathrm{kg}$ ) 满足关系式: $y=-100 x+5000$. 经 销售发现, 销售单价不低于成本价且不高于 30 元 $/ \mathrm{kg}$. 当每日销售量不低于 $4000 \mathrm{~kg}$ 时, 每千克成本将降低 1 元, 设板栗公司销售该板栗的日获利为 $w$ (元).
（1）请求出日获利 $w$ 与销售单价 $x$ 之间的函数关系式;
（2）当销售单价定为多少时, 销售这种板栗日获利最大? 最大利润为多少元?
（3）当 $w \geqslant 40000$ 元时, 网络平台将向板栗公司收取 $a$ 元 $/ \mathrm{kg}(a < 4)$ 的相关费用, 若此 时日获利的最大值为 42100 元, 求 $a$ 的值.
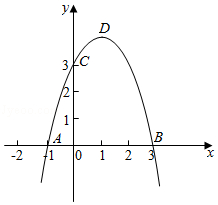
已知抛物线 $y=a x^{2}+b x+c$ 与 $x$ 轴交于点 $A(-1,0)$, 点 $B(3,0)$, 与 $y$ 铀交于点 $C(0$,3). 顶点为点 $D$.
（1）求抛物线的解析式;
(2) 若过点 $C$ 的直线交线段 $A B$ 于点 $E$, 且 $S_{\triangle A C E}: S_{\triangle C E B}=3: 5$, 求直线 $C E$ 的解析式;
(3) 若点 $P$ 在抛物线上, 点 $Q$ 在 $x$ 轴上, 当以点 $D, C, P, Q$ 为顶点的四边形是平行 四边形时, 求点 $P$ 的坐标;
(4) 已知点 $H\left(0, \frac{45}{8}\right), G(2,0)$, 在抛物线对称轴上找一点 $F$, 使 $H F+A F$ 的值最小. 此 时, 在抛物线上是否存在一点 $K$, 使 $K F+K G$ 的值最小? 若存在, 求出点 $K$ 的坐标; 若 不存在, 请说明理由.
