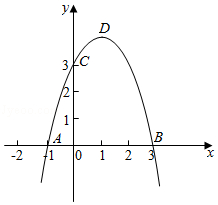
已知抛物线 $y=a x^{2}+b x+c$ 与 $x$ 轴交于点 $A(-1,0)$, 点 $B(3,0)$, 与 $y$ 铀交于点 $C(0$,3). 顶点为点 $D$.
（1）求抛物线的解析式;
(2) 若过点 $C$ 的直线交线段 $A B$ 于点 $E$, 且 $S_{\triangle A C E}: S_{\triangle C E B}=3: 5$, 求直线 $C E$ 的解析式;
(3) 若点 $P$ 在抛物线上, 点 $Q$ 在 $x$ 轴上, 当以点 $D, C, P, Q$ 为顶点的四边形是平行 四边形时, 求点 $P$ 的坐标;
(4) 已知点 $H\left(0, \frac{45}{8}\right), G(2,0)$, 在抛物线对称轴上找一点 $F$, 使 $H F+A F$ 的值最小. 此 时, 在抛物线上是否存在一点 $K$, 使 $K F+K G$ 的值最小? 若存在, 求出点 $K$ 的坐标; 若 不存在, 请说明理由.