单选题 (共 16 题 ),每题只有一个选项正确
$4$的平方根是
$\text{A.}$ $2$
$\text{B.}$ $16$
$\text{C.}$ $\pm 2$
$\text{D.}$ $\pm 16$
在式子 $\frac{x}{2}, \frac{x+y}{x-2 y}, \frac{x}{\pi}, \frac{2 x-y}{4}, \frac{1}{a}, 2 a$ 中,分式的个数在
$\text{A.}$ 1个
$\text{B.}$ 2个
$\text{C.}$ 3个
$\text{D.}$ 4个
若分式 $\frac{1}{2 x+4}$ 有意义,则 $x$ 的取值范围
$\text{A.}$ $x \geqslant 2$
$\text{B.}$ $x \geqslant-2$
$\text{C.}$ $x \neq-2$
$\text{D.}$ $x \neq 2$
给出四个数 $0, \sqrt{2}, 1,-2$,其中最大的数是
$\text{A.}$ 0
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ 1
$\text{D.}$ $-2$
下列四个命题中, 是真命题的是
$\text{A.}$ 同角的补角相等
$\text{B.}$ 相等的角是对顶角
$\text{C.}$ 三角形的一个外角大于任何一个内角
$\text{D.}$ 两条直线被第三条直线所截,内错角相等
小亮用天平秤得一个鸡蛋的质量为 50.47g,用四舍五入法将50.47精确到0.1的近似值为
$\text{A.}$ $50$
$\text{B.}$ $50.0$
$\text{C.}$ $50.4$
$\text{D.}$ $50.5$
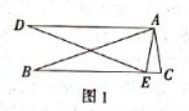
如图 1, $\triangle A B C \cong \triangle A D E$, 点 $E$ 在 $B C$ 边上, $\angle C A E=20^{\circ}$, 则 $\angle A E D$ 的度数为
$\text{A.}$ $60^{\circ}$
$\text{B.}$ $90^{\circ}$
$\text{C.}$ $80^{\circ}$
$\text{D.}$ $20^{\circ}$
把分式 $\frac{3 x-3 y}{x y}$ 中的 $x y$ 的值同时扩大为原来的 2 倍,则分式的值
$\text{A.}$ 不变
$\text{B.}$ 扩大为原来的 2 倍
$\text{C.}$ 扩大为原来的 4倍
$\text{D.}$ 缩小为原来的一半
估计 $\sqrt{5}+2$ 的值在
$\text{A.}$ 2 和 3 之间
$\text{B.}$ 3 和 4 之问
$\text{C.}$ 4 和 5 之间
$\text{D.}$ 5 和 6 之间
学完分式运算后,老师出了一道题: 化筒 $\frac{x+3}{x+2}+\frac{2-x}{x^2-4}$.
小明的做法是:
原式 $=\frac{(x+3)(x-2)}{x^2-4}-\frac{x-2}{x^2-4}=\frac{(x+3)(x-2)-x-2}{x^2-4}=\frac{x^2-8}{x^2-4}$;
小亮的做法是:
原式 $=(x+3)(x-2)+(2-x)=x^2+x-6+2-x=x^2-4$;
小芳的做法是:
原式 $=\frac{x+3}{x+2}-\frac{x-2}{(x+2)(x-2)}=\frac{x+3}{x+2}-\frac{1}{x+2}=\frac{x+3-1}{x+2}=1$.
对于这三名同学的做法,你的判断是
$\text{A.}$ 小明的做法正确
$\text{B.}$ 小亮的做法正确
$\text{C.}$ 小芳的做法正确
$\text{D.}$ 三名同学的做法都不正确
已知 $\sqrt{x+1}+|y-2|=0$, 代数式 $2 x y$ 的值为
$\text{A.}$ $0$
$\text{B.}$ $-4$
$\text{C.}$ $4$
$\text{D.}$ $-2$
化简 $\left(1-\frac{2 x-1}{x^2}\right) \div\left(1-\frac{1}{x^2}\right)$ 的结果为
$\text{A.}$ $\frac{x-1}{x+1}$
$\text{B.}$ $\frac{x+1}{x-1}$
$\text{C.}$ $\frac{x+1}{x}$
$\text{D.}$ $\frac{x-1}{x}$
说明命题 "如果 $a, b, c$ 是 $\triangle A B C$ 的三边,那么长为 $a-1, b-1, c-1$ 的三条 线段能构成三角形" 是假命题的反例可以是
$\text{A.}$ $a=2, b=2, c=3$
$\text{B.}$ $a=2, b=2, c=2$
$\text{C.}$ $a=3, b=3, c=4$
$\text{D.}$ $a=3, b=4$
巳知实数 $a, b$ 在数轴上对应的点如图 2 所示, 则下列式子正确的是
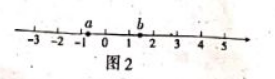
$\text{A.}$ $-a < -b$
$\text{B.}$ $a+b < 0$
$\text{C.}$ $|a| < |b|$
$\text{D.}$ $a-b>0$
如图 3-1, 已知线段 $a, \angle 1$, 求作 $\triangle A B C$, 使 $B C=a, \angle A B C=\angle B C A=$ $\angle 1$, 张雷的作法如图 3-2 所示, 则下列说法中一定正确的是。
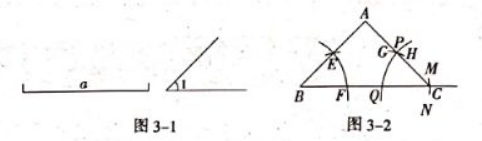
$\text{A.}$ 作 $\triangle A B C$ 的依据为 $\mathrm{ASA}$
$\text{B.}$ 弧 $E F$ 是以 $A C$ 长为半径画的
$\text{C.}$ 弧 $M N$ 是以点 $A$ 为圆心, $a$ 为半径画的
$\text{D.}$ 弧 $C H$ 昌以 $C P$ 长为半径画的
若方程 $\frac{3-2 x}{x-3}+\frac{2+m x}{3-x}=-1$ 无解, 则 $m$ 的值为
$\text{A.}$ $-1$
$\text{B.}$ 3
$\text{C.}$ $-1$ 或 3
$\text{D.}$ $-1$ 或 $-\frac{5}{3}$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若分式 $\frac{|x|-4}{4-x}$ 的值为 0 , 则 $x=$
如图 4, $E B$ 交 $A C$ 于 $M$, 交 $F C$ 于, $A B$ 交 $F C$ 于 $N, \angle E=\angle F=90^{\circ}, \angle B=\angle C, A E=A F$. 给 出下列结论:
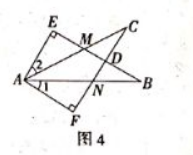
① $\angle 1=\angle 2$;
② $B E=C F$;
③ $\triangle A C N \cong \triangle A B M$;
④ $C D=D N$. 其中正确的结论有 (填序号)
观察下列等式:
等式 $1: \sqrt{\frac{1}{2}-\frac{1}{4}}=\frac{1}{2}$;
等式 $2: \sqrt{\frac{1}{3}-\frac{1}{9}}=\frac{\sqrt{2}}{3}$;
等式 $3: \sqrt{\frac{1}{4}-\frac{1}{16}}=\frac{\sqrt{3}}{4}$
猜想第5个等式为,
由以上观察研究,猜想:用含n的式子表示低n个等式所反映的运算规律为
所反映的运算规律为
先化简代数式 $\left(\frac{2}{a-1}-\frac{a+2}{a^2-1}\right) \div \frac{a}{a-1}$, 再带入一个你喜欢的求值.
阅读材料
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于$x$的分式方程$ \frac{a}{x-4}=1$ 的解为正数,求a的取值范围。
经过独立思考后,小杰和小哲开始交流思路如下:
小杰说:解这个x的方程,得 $x=a+4$ 有题意可得 $a+4>0$ 所以 $a>-4$
问题解决
小哲说:你考虑的不全面,还必须保证 $ x \neq 4 $ , 即 $ a+4 \neq 4 $
(1)请回答:( ) 的说法正确,并简述其正确的理由是 ( )
(2)参考上面的讨论,解决下面的问题
若关于x的方程 $ \frac{m}{x-3}-\frac{x}{3-x}=2$的解为非负数,求m的取值范围
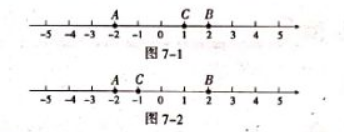
给出定义:数轴上顺次有三点 $A,C,B$,若C到点A的距离是点C到点B的距离的3倍,我们就称呼点C是(A,B)的“梦想点”。例如图7-1中,点A,B表示的数分别为-2,2,表示数1的点C是(A,B)的梦想点,图7-2中,点A,B表示的数分别为-2,2表示-1的点C是(B,A)的梦想点
【解决问题】
(1) 若数轴上 $M, N$ 两点所表示的数分的为 $m, n$, 且 $m, n$ 满足 $ | m+7| + 2|n-1|=0 $ 求(M.N)的梦想点表示的数
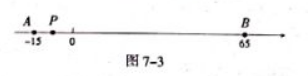
(2) 如图7-3, 在数轴上点 $A, B$ 表示的数分别为 - 15 和 65 , 点 $P$ 从点 $A$ 出发沿数轴向右运动
①若点 $P$ 运动到点 $B$ 佟止,则当 $P, A, B$ 中恰好有一个点为其余两个点的梦想点时,求这个点表示的数。
②若点P运动到B后,继续沿数轴向右运动的过程中,是否还存在点P,A,B中正好有一个点为其余两点的梦想点的情况?若存在,请直接写出此时以PA,PB为邻边长的长方形的周长,若不存在,请说明理由
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
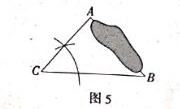
如图5,一块三角形模具的阴影部分已破损. 只要从残留的模具片中 度量出那些边、角,就可以不带残留的模具到店铺加工一块与原来的模具 $\triangle A B C$ 的形状和大小完全相同的枚具 $\triangle A^{\prime} B^{\prime} C^{\prime}$ ? 请简要说明理由. 作出模具 $\triangle A^{\prime} B^{\prime} C^{\prime}$ 的图形.
阅读理解
$\because \sqrt{4} < \sqrt{5} < \sqrt{9}$, 即 $2 < \sqrt{5} < 3, \therefore 1 < \sqrt{5}-1 < 2$.
$\therefore \sqrt{5}-1$ 的整数部分为 1 .
$\therefore \sqrt{5}-1$ 的小数部分为 $(\sqrt{5}-1)-1=\sqrt{5}-2$
解决问题:
已知$a$是 $\sqrt{19}-3$ 的整数部分,$b$是 $\sqrt{26}-2$的小数部分,求 $(-a)^3+(b+5)^2$ 的平方根
某商场11月初花费15000元购进一批某品牌英语点读笔,因深受顾客喜爱,销售一空,该商场于12月初又花费24000元购进一批同品质英语点读笔,且所有数量是11月初的1.5倍,但每支进价涨了10元
(1)求商场11月初购进英语点读笔多少支?
(2)11月份商场每支点读笔售价是270元,若12月份购买的点读笔全部卖完,且所获利利润是11月份利润的1.2倍,求12月份每支的售价
如图 6, 在 $\triangle A B E$ 中, $A B=A E, A D=A C, \angle B A D=\angle E A C, B C, D E$ 交于点$O$
(1)在不添加字母和辅助线的情况下,请你在图中找出一对全等三角形并写出证明它们全等的过程。
(2)求证:OD=OC
