解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
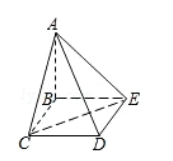
四棱雉 $A-B C D E$ 中, 底面 $B C D E$ 为矩形, 侧面 $A B C \perp$ 底面 $B C D E, B C=2$
, $C D=\sqrt{2}, \quad A B=A C$.
( I ) 证明: $\mathrm{AD} \perp \mathrm{CE}$;
(II) 设 $\mathrm{CE}$ 与平面 $\mathrm{ABE}$ 所成的角为 $45^{\circ}$, 求二面角 $C-A D-E$ 的大小.
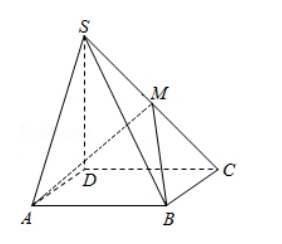
如图, 四棱雉 S- $A B C D$ 中, 底面 $A B C D$ 为矩形, $S D \perp$ 底面 $A B C D$, $A D=\sqrt{2}, D C=S D=2$, 点 $M$ 在侧棱 $S C$ 上, $\angle A B M=60^{\circ}$
(I) 证明: $M$ 是侧棱 SC 的中点;
(II)求二面角 $\mathrm{S}-\mathrm{AM}-\mathrm{B}$ 的大小.
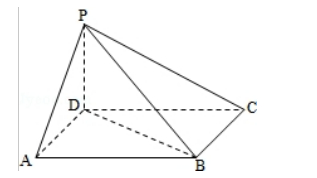
如图, 四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 为平行四边形, $\angle D A B=60^{\circ}$
, $A B=2 A D, P D \perp$ 底面 $A B C D$.
( I ) 证明: $\mathrm{PA} \perp \mathrm{BD}$;
(II) 若 $P D=A D$, 求二面角 $A^{-} P B-C$ 的余弦值.
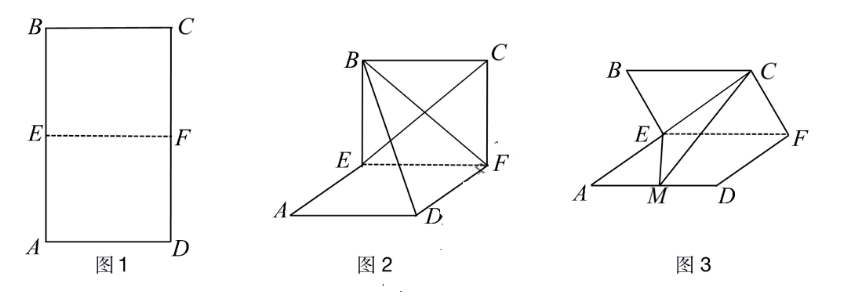
如图 1, 矩形 $A B C D$, 点 $E, F$ 分别是线段 $A B, C D$ 的中点, $A B=4, A D=2$, 将 矩形 $A B C D$ 沿 $E F$ 翻折
(I) 若所成二面角的大小为 $\frac{\pi}{2}$ (如图 2) , 求证: 直线 $C E \perp$ 面 $D B F$;
(II) 若所成二面角的大小为 $\frac{\pi}{3}$ (如图 3), 点 $M$ 在线段 $A D$ 上, 当直线 $B E$ 与面 $E M C$ 所 成角为 $\frac{\pi}{4}$ 时, 求二面角 $D-E M-C$ 的余弦值.
如图,在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 为梯形, $A B=2 A D=2 D C, A B / /$ $D C, A B \perp A D$, 平面 $P C B \perp$ 平面 $A B C D$.
(1) 证明: $P B \perp A C$;
(2) 若 $\triangle P C B$ 为正三角形, 求二面角 $B P A-C$ 的正弦值.

如图所示, 在等腰梯形 $A B C D$ 中, $A B / / C D, B C=C D=2, C F=1, \angle B C D=120^{\circ}$, 四边形 $A C F E$ 为矩形且满足 $A E \perp$ 平面 $A B C D$.
(1) 证明: $E F \perp$ 平面 $B C F$ ;
(2) 若 $M$ 是 $E F$ 中点, 求点 $C$ 到平面 $B F M$ 的距离.
