解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知抛物线$C:y^2=3x$ 的焦点为F,斜率为$\dfrac{3}{2}$的直线l与C的交点为A,B,与x轴的交点为P.
(1)若$|AF|+|BF|=4$,求 $l$ 的方程;
(2)若$\overrightarrow{A P}=3 \overrightarrow{P B}$ ,求$|AB|$.
己知抛物线 $C: \quad x^{2}=2 p y(p>0)$ 的焦点为 $F$, 且 $F$ 与圆 $M: x^{2}+(y+4)^{2}=1$ 上点的 距离的最小值为 $4 .$
(1)求 p;
(2)若点 $\mathrm{P}$ 在 $\mathrm{M}$ 上, $\mathrm{PA}, \mathrm{PB}$ 是 $\mathrm{C}$ 的两条切线, $\mathrm{A}, \mathrm{B}$ 是切点, 求 $\triangle \mathrm{PAB}$ 的最大值.
已知圆 $C:(x-1)^{2}+y^{2}=16$, 点 $F(-1,0), P$ 是圆 $C$ 上一动点, 若线段 $P F$ 的垂直平分线和 $C P$ 相交于点 $M$.
(1) 求点 $M$ 的轨迹方程 $E$.
(2) $A, B$ 是 $M$ 的轨迹方程与 $x$ 轴的交点 (点 $A$ 在点 $B$ 左边), 直线 $G H$ 过点 $T(4,0)$ 与轨迹 $E$ 交 于 $G, H$ 两点, 直线 $A G$ 与 $x=1$ 交于点 $N$, 求证: 动直线 $N H$ 过定点.
双曲线的中心为原点 $\mathrm{O}$, 焦点在 $\mathrm{x}$ 轴上, 两条渐近线分别为 $\mathrm{I}_{1}, \mathrm{I}_{2}$, 经过右焦点 $F$ 垂直于 $I_{1}$ 的直线分别交 $l_{1}, I_{2}$ 于 $A, B$ 两点. 已知 $|\overrightarrow{O A}| 、|\overrightarrow{A B}|$ 、
$|\overrightarrow{\mathrm{OB}}|$ 成等差数列, 且 $\overrightarrow{\mathrm{BF}}$ 与 $\overrightarrow{\mathrm{FA}}$ 同向.
(I)求双曲线的离心率;
(II ) 设 $A B$ 被双曲线所截得的线段的长为 4 , 求双曲线的方程.
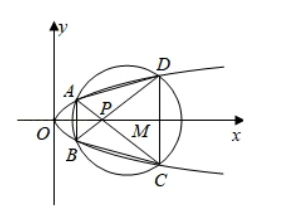
如图, 已知抛物线 $E: y^{2}=x$ 与圆 $M:(x-4)^{2}+y^{2}=r^{2}(r>0)$ 相交 于 $A 、 B 、 C 、 D$ 四个点.
( I ) 求 $\mathrm{r}$ 的取值范围;
(II ) 当四边形 $A B C D$ 的面积最大时, 求对角线 $A C 、 B D$ 的交点 $P$ 的坐标.
设 $F_{1}, F_{2}$ 分别是椭圆 $E: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 的左、右焦点, 过 $F_{1}$ 斜率为 1 的直线 $\ell$ 与 $E$ 相交于 $A, B$ 两点, 且 $\left|A F_{2}\right|,|A B|,\left|B_{2}\right|$ 成等差数列
(1) 求 $\mathrm{E}$ 的离心率;
(2) 设点 $P(0,-1)$ 满足 $|P A|=|P B|$, 求 $E$ 的方程.