一、单选题 (共 8 题 ),每题只有一个选项正确
1. 已知全集 , 则集合 为
2. 已知直线 、、 与平面 、, 下列命题正确的是
若 , 则
若 , 则
若 , 则
若 , 则
3. 若抛物线 上一点 到焦点的距离是 , 则 的值为
4. 在党的二十大报告中, 习近平总书记提出要发展 “高质量教育”, 促进城乡教育均衡发展. 某地区教育行政部门积极响应党中央号召, 近期将安排甲、乙、丙、丁 4 名教育专家前往某省教育相对落后的三个地区指导教育教学工作, 则每个地区至少安排 1 名专家的概率为
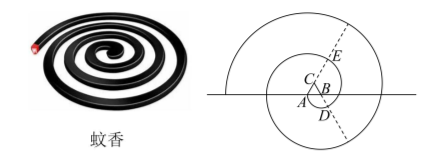
5. 蚊香具有悠久的历史, 我国蚊香的发明与古人端午节的习俗有关.如图为某校数学社团用数学软件制作的“蚊香”. 画法如下: 在水平直线上取长度为 1 的线段
, 作一个等边三角形
, 然后以点
为圆心,
为半径逆时针画圆弧交线段
的延长线于点
(第一段圆弧), 再以点
为圆心,
为半径逆时针画圆弧交线段
的延长线于点
, 再以点
为圆心,
为半径逆时针画圆弧以此类推,当得到的“蚊香”恰好有 15 段圆弧时, “蚊香”的长度为
6. 已知圆 , 直线 与圆 交于 两点. 若 为直角三角形, 则
7. 现有甲、乙两组数据, 每组数据均由六个数组成, 其中甲组数据的平均数为 3 , 方差为 5 , 乙组数据的平均数为 5 , 方差为 3 . 若将这两组数据混合成一组, 则新的一组数据的方差为
3.5
4
4.5
5
8. “曼哈顿距离”是十九世纪的赫尔曼・闵可夫斯基所创词汇, 定义如下: 在直角坐标平面上任意两点 的曼哈顿距离为: .已知点 在圆 上,点 在直线 上, 则 的最小值为
二、多选题 (共 3 题 ),每题有多个选项正确
9. 设集合 , 则下列图象能表示集合 到集合 的函数关系的有
10. 已知二项展开式 , 下列说法正确的有
的展开式中的常数项是 56
的展开式中的各项系数之和为 0
的展开式中的二项式系数最大值是 70
, 其中 为虚数单位
11. 在 中, 若 , 则
对任意的 , 都有
对任意的 , 都有
存在 , 使 成立
存在 , 使 成立
三、填空题 (共 3 题 ),请把答案直接填写在答题纸上
12. 已知单位向量 满足 , 则
13. 定义两个点集 、 之间的距离集为 , 其中 表示两点 、 之间的距离, 已知 、, 若 , 则 的值为
14. 已知 , 过点 倾斜角为 的直线 交 于 、 两点 ( 在第一象限内), 过点 作 轴, 垂足为 , 现将 所在平面以 轴为翻折轴向纸面外翻折, 使得 上平面下平面, 则几何体 外接球的表面积为
四、解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
15. 已知函数 .
(1) 当 时, 求函数 的单调区间;
(2) 当 时, 求函数 的最大值.
16. 设 为数列 的前 项和, 已知 是首项为 、公差为 的等差数列.
(1) 求 的通项公式;
(2) 令 为数列 的前 项积, 证明: .
17. 最新研发的某产品每次试验结果为成功或不成功, 且每次试验的成功概率为 . 现对该产品进行独立重复试验, 若试验成功, 则试验结束; 若试验不成功, 则继续试验, 且最多试验 8 次. 记 为试验结束时所进行的试验次数, 的数学期望为 .
(1) 证明: ;
(2) 某公司意向投资该产品, 若 , 每次试验的成本为 元, 若试验成功则获利 元, 则该公司应如何决策投资? 请说明理由.
18. 已知椭圆
的左、右焦点分别为
、, 离心率为
, 经过点
且倾斜角为
的直线
与椭圆交于
、 两点 (其中点
在
轴上方),
的周长为 8 .
(1) 求椭圆
的标准方程;
(2) 如图, 将平面
沿
轴折叠, 使
轴正半轴和
轴所确定的半平面 (平面
) 与
轴负半轴和
轴所确定的半平面 (平面
) 互相垂直.
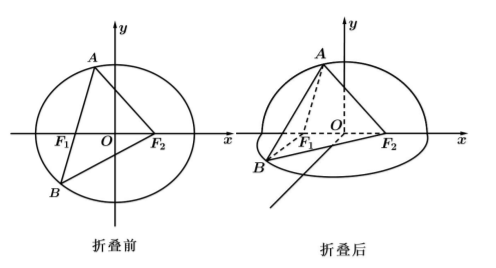
(1)若
, 求异面直线
和
所成角的余弦值;
(2) 是否存在
, 使得折叠后
的周长为
? 若存在, 求
的值; 若不存在, 请说明理由.
19. 已知定义域为 的函数 满足: 对于任意的 , 都有 , 则称函数 具有性质 .
(1) 判断函数 是否具有性质 ; (直接写出结论)
(2) 已知函数 , 判断是否存在 , 使函数 具有性质 ? 若存在, 求出 的值; 若不存在, 说明理由;
(3) 设函数 具有性质 , 且在区间 上的值域为 .
函数 , 满足 , 且在区间 上有且只有一个零点.
求证: .