一、单选题 (共 8 题 ),每题只有一个选项正确
1. 已知集合 , 则
2. 命题“ ” 的否定为
3. 三名同学到五个社区参加社会实践活动, 要求每个社区有且只有一名同学, 每名同学至多去 两个社区,则不同的派法共有
90 种
180 种
125 种
243 种
4. 已知向量 , 且 , 若 , 则实数 的值为
0
-1
5. 已知点 是角 的终边上一点. 则
3 或
3
6. 如图, 长方体
中,
, 若直线
与平面
所成的角为
, 则直线
与直线
所成的角为

7. 若直线 与圆 交于 两点, 则当 周 长最小时,
1
-1
8. 已知 , 若对任意的 恒成立, 则实数 的最小值为
e
二、多选题 (共 4 题 ),每题有多个选项正确
9. 某企业秉承“科学技术是第一生产力”的发展理念, 投人大量科研经费进行技术革新,该企业统计了最近 6 年投入的年科研经费
(单位: 百万 元) 和年利润
(单位: 百万元) 的数据, 并绘制成如图所示的散点图. 已知
的平均值分别为
. 甲统计员得到的回归方程为
1.
; 乙统计员得到的回归方程为
; 若甲、乙二人计 算均末出现错误, 则以下结论正确的为
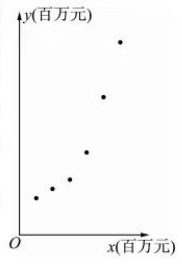
当投入年科经费为 20 (百万)按乙统计员的回归方程可得年 利润估计值为 75.6 (百万元) (取 )
方程 比方程 拟合效果好
与 正相关
10. 已知定义域为 的偶函数 的图象是连续不间断的曲线, 且 , 对任意的 恒成立, 则
在 上单调递增
是以 4 为周期的函数
的图象关于直线 对称
在区间 上的零点个数为 100
11. 将函数 图象上所有点的横坐标变为原来的 , 再向左平移 个单位长度, 得到函数 的图象, 若对任意的 , 均有 成立, 则
的地大值为 1
的最小值为
在 上单调递增
对任意的 , 均有 成立
12. 已知双曲线 的左、右焦点分别为 , 其一条渐近线为 , 直线 过点 且与双曲线 的右支交于 两点, 分别为 和 的 内心, 则
直线 倾斜角的取值范围为
点 与点 始终关于 轴对称
三角形 为直角三角形
三角形 面积的最小值为
三、填空题 (共 5 题 ),请把答案直接填写在答题纸上
13. 若 ( 为虚数单位) 为纯虚数, 则实数 的值为
14. 已知函数 满足: (1) 对 ; (2) . 请写出一个符 合上述两个条件的函数
15. 已知等差数列 的前 项和为 , 且 , 则满足 的正整数 的 为
16. 在三棱锥 中, 底面 是边长为 的正三角形, , 点 为 的 垂心, 且 平面 , 则三棱雉 的外接球的体积为
17. 在(1) ; (2) ; (3) 三个条件中任选一个, 补充 到下面问题的横线处, 并解答.
已知数列 的前 项和为 , 且 ,
(1) 求 ;
(2) 设 , 求数列 的前 项和 .
注: 如果选择多个条件解答, 按第一个解答计分.
四、解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
18. 已知 为 的内角 所对的边, 向量 , 且 .
(1) 求角 ;
(2) 若 的面积为 为 中点, 求线段 的长.
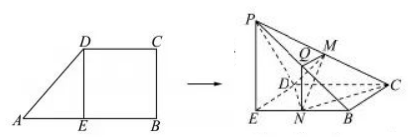
19. 如图, 梯形
中,
, 垂 足为点
, 将
沿
折起, 使得点
到点
的位置, 且
, 连接
,
分别为
和
的中点.
(1) 证明:
平面
;
(2) 求二面角
的正弦值.
20. 乒乓球是我国的国球, “乒兵精神”激励了一代又一代国人.为弘扬国球精神,传承乒 乓球文化, 强健学生体魄, 某中学举行了乒乓球单打比赛. 比赛采用 7 局 4 胜制, 每局比赛为 11 分制, 选手只要得到至少 11 分, 并且领先对方至少 2 分 (包括 2 分), 即赢得该局比赛. 在 一局比赛中, 每人只发 2 个球就要交换发球权, 如果双方比分为 后, 每一个球就要交 换一个发球权, 经过紧张的角逐, 甲、乙两位选手进入了决赛.
(1) 若甲贏得每局比赛的概率为 , 求甲以 贏得比赛的概率;
(2) 若在某一局比赛中, 双方战成 , 且甲获得了第一球的发球权, 若甲发球时甲贏 1 分 的概率为 , 乙发球时甲贏 1 分的概率为 , 求两人打了 个球后, 甲贏得了该 局比赛的概率.
21. 已知椭圆 的离心率为 , 且经过点 .
(1) 求椭圆 的方程;
(2) 若过点 的直线 与椭圆 交于 两点, 点 关于 轴的对称点为 , 求 面积的最大值.
22. 已知函数 .
(1) 当 时,求 的单调区间;
(2) 证明: 当 时, 对任意的 恒成立.