单选题 （共 8 题 ），每题只有一个选项正确
下列函数中, 是奇函数且在其定义域上为增函数的是
$\text{A.}$ $y=\sin x$
$\text{B.}$ $y=x|x|$
$\text{C.}$ $y=x^{\frac{1}{2}}$
已知定义在 $R$ 上的函数 $f(x)$ 的图象连续不断, 有下列四个命题:
甲: $f(x)$ 是奇函数;
乙: $f(x)$ 的图象关于直线 $x=1$ 对称;
丙: $f(x)$ 在区间 $[-1,1]$ 上单调递减;
丁：函数 $f(x)$ 的周期为 2 .
如果只有一个假命题, 则该命题是
$\text{A.}$ 甲
$\text{B.}$ 乙
$\text{C.}$ 丙
$\text{D.}$ 丁
已知函数 $f(x)=\left(\mathrm{e}^x-\mathrm{e}^{-x}\right) \cos x+2$ 在 $[-1,1]$ 上的最大值和最小值分别为 $M, N$, 则 $M+N=$
$\text{A.}$ -2
$\text{B.}$ 0
$\text{C.}$ 2
$\text{D.}$ 4
函数 $y=\frac{x \sin x}{\mathrm{e}^{|x|}}$ 的图象大致为
$\text{A.}$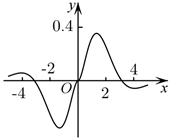 
$\text{B.}$ 
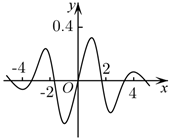$\text{C.}$ 
$\text{D.}$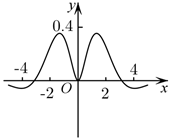 
已知定义域是 $\boldsymbol{R}$ 的函数 $f(x)$ 满足: $\forall x \in \mathbf{R}, f(4+x)+f(-x)=0, f(1+x)$ 为偶函数, $f(1)=1$, 则 $f(2023)=$
$\text{A.}$ 1
$\text{B.}$ -1
$\text{C.}$ 2
$\text{D.}$ -3
已知函数 $f(x)=3^{|x-2 \mid}+x^2-4 x$ ，且 $f\left(\log _2 a\right)>f(3)$ ， 则实数 $a$ 的取值范围为
$\text{A.}$ $(-\infty, 2) \cup(8,+\infty)$
$\text{B.}$ $(0,2)$
$\text{C.}$ $(0,2) \cup(8,+\infty)$
$\text{D.}$ $(8,+\infty)$
若 $f(x)$ 是定义域为 $(0,+\infty)$ 上的单调函数, 且对任意实数 $x \in(0,+\infty)$ 都有 $f\left[f(x)-\frac{1}{\mathrm{e}^x}\right]=\frac{1}{\mathrm{e}}+1$, 其中 e 是自然对数的底数, 则 $f(\ln 3)=$
$\text{A.}$ 4
$\text{B.}$ $\frac{4}{3}$
$\text{C.}$ $\mathrm{e}+2$
$\text{D.}$ $\frac{1}{3}$
已知函数 $f(x)$ 的定义域为 $\mathbf{R}, f(2+x)=f(-x), f(-2)=-f(4)$, 且 $f(x)$ 在 $[1,+\infty)$ 上递增, 则 $x f(x-1)>0$ 的解集为
$\text{A.}$ $(-2,0) \cup(4,+\infty)$
$\text{B.}$ $(-\infty,-1) \cup(5,+\infty)$
$\text{C.}$ $(-\infty,-2) \mathrm{U}(4,+\infty)$
$\text{D.}$ $(-1,0) \cup(5,+\infty)$
多选题 （共 4 题 ），每题有多个选项正确
已知函数 $f(x)=\frac{a x}{1-x^2}$, 则
$\text{A.}$ $f\left(\frac{1}{x}\right)=f(x)$
$\text{B.}$ 对任意实数 $a$ ，函数 $f(x)$ 为奇函数
$\text{C.}$ 存在实数 $a$, 使得 $f(x)$ 为偶函数
$\text{D.}$ $a>0$ 时, $f(x)$ 在区间 $(0,1)$ 上为单调递增函数
给出下列说法, 错误的有
$\text{A.}$ 若函数 $f(x)=\frac{k-3^x}{1+k \cdot 3^x}$ 在定义域上为奇函数, 则 $k=1$
$\text{B.}$ 已知 $f(x)=\lg \left(x^2+2 x+a\right)$ 的值域为 $\mathbf{R}$, 则 $a$ 的取值范围是 $a>1$
$\text{C.}$ 已知函数 $f(x)$ 满足 $f(x+1)=f(x-1)$, 且 $f(-1)=5$, 则 $f(3)=5$
$\text{D.}$ 已知函数 $f(x)=1+\log _3 x, x \in[1,9]$, 则函数 $y=f^2(x)+f\left(x^2\right)$ 的值域为 $[2,14]$
定义在 $R$ 上的奇函数 $f(x)$ 满足 $f(x+2)=-f(x)$, 且当 $x \in(0,1]$ 时, $f(x)=1-x$, 则
$\text{A.}$ $f(x)$ 是周期函数
$\text{B.}$ $f(x)$ 在 $(-1,1)$ 上单调递减
$\text{C.}$ $f(x)$ 的图象关于直线 $x=3$ 对称
$\text{D.}$ $f(x)$ 的图象关于点 $(2,0)$ 对称
记函数 $f(x)$ 与 $g(x)$ 的定义域的交集为 $I$. 若存在 $x_0 \in I$, 使得对任意 $x \in I$, 不等式
$[f(x)-g(x)]\left(x-x_0\right) \geq 0$ 恒成立, 则称 $(f(x), g(x))$ 构成 " $M$ 函数对". 下列所给的两个函数能构成 " $M$ 函数对"的有
$\text{A.}$ $f(x)=\ln x, g(x)=\frac{1}{x}$
$\text{B.}$ $f(x)=e^x, g(x)=\mathrm{e} x$
$\text{C.}$ $f(x)=x^3, g(x)=x^2$
$\text{D.}$ $f(x)=x+\frac{1}{x}, g(x)=3 \sqrt{x}$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
定义在 $\mathbf{R}$ 上的奇函数 $f(x)$, 当 $x \geq 0$ 时, $f(x)=2^x-a \cdot 2^{-x}$,当 $x < 0$ 时, $f(x)=$
已知函数 $f(x)=a x^3-\ln \left(\sqrt{x^2+1}+x\right)+3 \sin x+7$, $x \in[-2023,2023]$ 的最大值为 $M$, 最小值为 $m$, 则 $M+m=$
已知函数 $f(x)$ 及其导函数 $f^{\prime}(x)$ 的定义域均为 R , 若 $f(x+1)$ 是偶函数, $g(x)=(x-1) f^{\prime}(x)-1$ 恰有四个零点, 则这四个零点的和为
已知 $f(x)$ 的定义域为 $(0,+\infty)$ 且 $f(2)=2$, 对于任意正数 $x_1, x_2$ 都有 $f\left(x_1 x_2\right)=f\left(x_1\right)+f\left(x_2\right)-1$, 且当 $x>\frac{1}{2}$时, $f(x)>0$, 则不等式 $f(x) \leq 3$ 的解集为