解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $1=d_1 < d_2 < \cdots < d_k=n$ 是合数 $n$ 的全部正因数,若对任意 $1 \leq i \leq k-2$ ,均有 $d_i \mid d_{i+1}+d_{i+2}$ ,求 $n$.
设 $x_1, x_2, \cdots, x_{2023}$ 为两两不等的正实数,使得对每个 $n=1,2, \cdots, 2023$ ,
$$
a_n=\sqrt{\left(x_1+x_2+\cdots+x_n\right)\left(\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n}\right)}
$$
都是一个整数. 求证: $a_{2023} \geq 3034$.
设 $n$ 是一个正整数. "日式三角"是将 $1+2+\cdots+n$ 个圆排成正二角形的形状,使得对 $i=1,2, \cdots, n$ ,从上到下的第 $i$行恰有 $i$ 个圆且其中恰有一个被染为红色. 在日式三角内,"忍者路径"是指一串由 $n$ 个圆组成的序列,从最上面一行的圆开始,每次从当前圆连接到它下方相邻的两个圆之一,直到到达最下面一行的某个圆为止. 下图为一个 $n=6$ 的日式三角,其中画有一条包含两个红色圆的忍者路径.
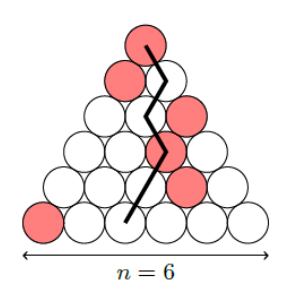
求最大的整数 $k$ (用 $n$ 表示),使得在每个日式三角中都存在一条忍者路径,它包含至少 $k$ 个红色圆.
设 $A B C$ 是一个正二角形. 点 $A_1, B_1, C_1$ 在二角形 $A B C$ 的内部,且满足 $B A_1=A_1 C, C B_1=B_1 A, A C_1=C_1 B$ ,以及
$$
\angle B A_1 C+\angle C B_1 A+\angle A C_1 B=480^{\circ} .
$$
设直线 $B C_1$ 与 $C B_1$ 交于点 $A_2$ ,直线 $C A_1$ 与 $A C_1$ 交于点 $B_2$ ,直线 $A B_1$ 与 $B A_1$ 交于点 $C_2$.
求证: 若三角形 $A_1 B_1 C_1$ 的三边长度两两不等,则三角形 $A A_1 A_2, B B_1 B_2$ 和 $C C_1 C_2$ 的外接圆都经过两个公共点.