单选题 (共 16 题 ),每题只有一个选项正确
四个数 $-1,0,-3,2$ 中, 最小的数是
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ -3
$\text{D.}$ 2
某地一天的最高气㵊是 $6{ }^{\circ} \mathrm{C}$, 最低乞湿是 $-4^{\circ} \mathrm{C}$, 则该地这天的温差是
$\text{A.}$ $6^{\circ} \mathrm{C}$
$\text{B.}$ $-6^{\circ} \mathrm{C}$
$\text{C.}$ $10^{\circ} \mathrm{C}$
$\text{D.}$ $-10^{\circ} \mathrm{C}$
若关于 $x$ 的方程 $2 x-m=x-2$ 的解为 $x=3$, 则 $m$ 的值为
$\text{A.}$ -5
$\text{B.}$ 5
$\text{C.}$ -7
$\text{D.}$ 7
如图, 将三角形 $A B C$ 绕点 $A$ 逆时针旋转 $85^{\circ}$ 得到三角形 $A B^{\prime} C^{\prime}$, 若 $\angle C^{\prime} A B^{\prime}=60^{\circ}$, 则 $B^{\prime}$ $\angle C A B^{\prime}=$
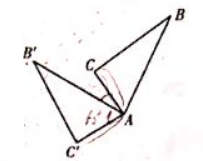
$\text{A.}$ $35^{\circ}$
$\text{B.}$ $30^{\circ}$
$\text{C.}$ $25^{\circ}$
$\text{D.}$ $15^{\circ}$
对下列代数式作出解释, 其中不正确的是
$\text{A.}$ $a-b$ : 今年小明 $b$ 岁.小明的爸爸 $a$ 岁,小明比他爸爸小 $(a-b)$ 岁
$\text{B.}$ $a-b$ : 今年小明 $b$ 岁, 小明的贫爸 $a$ 岁, 则小明出生时, 他爸爸为 $(a-b)$ 岁
$\text{C.}$ $a b:$ 长方形的长为 $a \mathrm{~cm}$, 宽为 $b \mathrm{~cm}$, 长方形的面积为 $a b \mathrm{~cm}^2$
$\text{D.}$ $a b$ :三角形的一边长为 $a \mathrm{~cm}$, 该边上的高为 $b \mathrm{~cm}$, 此三角形的面积为 $a b \mathrm{~cm}^2$
下列计算正确的是
$\text{A.}$ $7 a^2+3 a+8-\left(5 a^2-3 a+8\right)=2 a^2$
$\text{B.}$ $3 a+5 b-3 c-3 a+7 b-6 c=12 b-9$
$\text{C.}$ $3 x-2 y-[4 x-3(x-y)]=2 x-5 y$
$\text{D.}$ $5(a+b)+4(a+b)-12(a-b)=-3 a-3 b$
下列判断错误的是
$\text{A.}$ 多项式 $5 x^2-2 x+4$ 是二次三项式
$\text{B.}$ 单项式 $-a^2 b^3 c^4$ 的系数是 -1 , 次数是 9
$\text{C.}$ 式子 $m+5, a b, x=1,-2$ 都是代数式
$\text{D.}$ 当 $k=3$ 时, 关于 $x, y$ 的代数式 $(-3 k x y+3 y)+(9 x y-8 x+1)$ 中不含二次项
下列变形错误的是
$\text{A.}$ 如果 $x+7=26$, 那么 $x+5=24$
$\text{B.}$ 如果 $3 x+2 y=2 x-y$, 那么 $3 x+3 y=2 x$
$\text{C.}$ 如果 $2 a=5 b$, 那么 $2 a c=5 b c$
$\text{D.}$ 如果 $3 x=4 y$, 那么 $\frac{3 x}{a^2}=\frac{4 y}{a^2}$
已知 $A=a^2+b^2-c^2, B=-2 a^2-b^2+3 c^2$, 且 $A+B+C=0$, 则 $C=$
$\text{A.}$ $a^2-2 c^2$
$\text{B.}$ $a^2+2 c^2$
$\text{C.}$ $-a^2-2 c^2$
$\text{D.}$ $-a^2+2 c^2$
已知 $a, b, c$ 是三个有理数, 且 $a b c < 0, a+b < 0, a+b+c-1=0$, 下列式子一定正确的是
$\text{A.}$ $|a|>|b+c|$
$\text{B.}$ $c-1 < 0$
$\text{C.}$ $|a+b-c|-|a+b-1|=c-1$
$\text{D.}$ $b+c>0$
已知 $\angle A O B=30^{\circ}$, 自 $\angle A O B$ 顶点 $O$ 引射线 $O C$, 若 $\angle A O C: \angle A O B=4: 3$, 则 $\angle B O C$ 的度数是
$\text{A.}$ $10^{\circ}$
$\text{B.}$ $40^{\circ}$ 或 $30^{\circ}$
$\text{C.}$ $70^{\circ}$
$\text{D.}$ $10^{\circ}$ 或 $70^{\circ}$
某商店在甲批发市场以每包 $m$ 元的价格进了 40 包茶叶, 又在乙批发市场以每包 $n(m>n)$ 元的价格进了同样的 60 包茶叶,如果商家以每包 $\frac{m+n}{2}$ 元的价格卖出这种茶叶,卖完后, 这家商店
$\text{A.}$ 盈利了
$\text{B.}$ 亏损了
$\text{C.}$ 不盈不亏
$\text{D.}$ 盈亏不能确定
某项工程甲单独完成要 45 天, 乙单独完成要 30 天, 若乙先单独干 22 天, 利下的由甲单独完成. 求甲、乙一共用儿天可以完成全部工作. 若设甲、乙一共用 $x$ 天完成,则符合题意的方程是
$\text{A.}$ $\frac{x-22}{45}+\frac{22}{30}=1$
$\text{B.}$ $\frac{x+22}{30}+\frac{22}{45}=1$
$\text{C.}$ $\frac{x+22}{45}+\frac{22}{30}=1$
$\text{D.}$ $\frac{x}{5 x}+\frac{x-22}{5}=1$
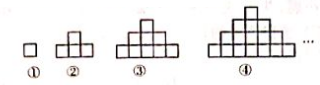
如图,用火柴棒摆出一列正方形图案,第 1 个图案用了 4 根,第 2 个图案用了 12 根,第 3 个图案用了 24 根,按照这种方式摆下去,摆出第6个团用的火柴根数是

$\text{A.}$ 84
$\text{B.}$ 81
$\text{C.}$ 78
$\text{D.}$ 76
如图, 在数轴上有 $A, B, C, D$ 四个整数点(即各点均表示整数), 且 $2 A B=B C=3 C D$, 若 $A, D$ 两点表示的数分别为 -5 和 6 , 且 $A C$ 的中点为 $E, B D$ 的中点为 $M, B, C$ 之间距点 $B$ 的距离为 $\frac{1}{3} B C$ 的点为 $N$, 则该数轴的原点为

$\text{A.}$ E
$\text{B.}$ F
$\text{C.}$ M
$\text{D.}$ N
填空题 (共 3 题 ),请把答案直接填写在答题纸上
对于有理数 $a, b$, 规定一种新运算: $a \oplus b=a b+b$, 则 $(x-4) \oplus 3=-6$ 的解为
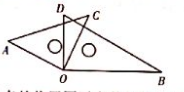
如图, 将一副直角三角尺叠在一起, 使直角顶点重合于点 $O$, 则 $\angle A O B+\angle D O C=$度.
$A, B$ 两动点分別在数轴上表示 $-6,12$ 的点的位置同时向数轴负方向运动, 它们的速度分别是 2 个单位长度每秒、4 个单位长度每秒,另一动点 $C$ 也在数轴上表示 12 的点的位置同时向数轴负方向运动,当遇到点 $A$ 后, 立即返回向点 $B$ 运动, 遇到点 $B$ 后又立即返回向点 $A$ 运动, 已知点 $C$-直以 8 个单位长度每秒的速度匀速运动, 如此往返, 直到点 $B$ 追上点 $A$ 时, 点 $C$ 立即停止运动. 那么点 $C$ 从开始运动到停止运动所用的时间为秒 ________ , 运动的路程是 ________ 个单位长度.
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算:
(1) $40 \div(-8)+(-3) \times(-2)^2+17$;
(2) $(-2)^2-|-7|+3-2 \times\left(-\frac{1}{2}\right)$.
已知 $A=3 x^2+3 y^2-5 x y, B=2 x y-3 y^2+4 x^2$.
(1) 化简 $2 B-A$;
(2) 已知 $-a^{x-21} b^2$ 与 $\frac{1}{3} a b^{y}$ 是同类项, 求 $2 B-A$ 的值.
若方程 $\frac{1-2 x}{6}+\frac{x+1}{3}=1-\frac{2 x+1}{4}$ 与关于 $x$ 的方程 $x+\frac{6 x-a}{3}=\frac{a}{6}-3 x$ 的解相同, 求 $a$ 的值.
已知点 $C$ 在直线 $A B$ 上. 点 $M, N$ 分别为 $A C, B C$ 的中点.
(1) 若点 $C$ 在线段 $A B$ 上, $A C=6 \mathrm{~cm}, M B=10 \mathrm{~cm}$, 求线段 $B C, M N$ 的长;
(2) 若点 $C$ 在线段 $A B$ 的延长线上, 且满足 $A C-B C=b \mathrm{~cm}$, 求 $M N$ 的长.
某公园门票价格规定如下表:

某校七年级(一)、(二)两个班共 104 人去逛公园, 其中 (一) 班人数较少, 不足 50 人. 经估算 若两个班都以班为单位购票, 则一共应付 1240 元, 问:
(1) 两班各有多少学生?
(2) 如果两班联合起来,作为一个团体购票,可省多少钱?
(3) 如果七年级 (一)班单独组织去公园,作为组织者的你将如何购票才最省钱?
如图是由边长为1的若干正方形拼成的图像,其中第一个图像有1个正方形组成,周长为4,第二个图像由4个正方形组成,变成为10,第3个图像由9个正方形组成,变成为16.。。
(1) 第4 个图形由 个正方形组成。周长为
(2) 第n 个图形由 个正方形组成。周长为
(3) 若某个图像的周长为58,该图形由多少个正方形拼成?
如图①, 在长方形 $A B C D$ 中, $A B=12 \mathrm{~cm}, B C=6 \mathrm{~cm}$. 点 $P$ 沿 $A B$ 边从点 $A$ 开始向点 $B$ 以 $2 \mathrm{~cm} / \mathrm{s}$ 的速度移动,点 $Q$ 沿 $D A$ 边从点 $D$ 开始向点 $A$ 以 $1 \mathrm{~cm} / \mathrm{s}$ 的速度移动.
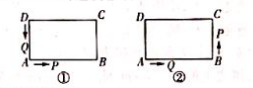
设点 $P, Q$ 同时出发,用 $t(\mathrm{~s})$ 表示移动的时间.
【发现】 $D Q=$ $\mathrm{cm}, A P=$ $\mathrm{cm}$. (用含 $t$ 的代数式表示)
【拓展】 (1) 如图①, 当 $t=$ $\mathrm{s}$ 时,线段 $A Q$ 与线段 $A P$ 相等;
(2) 如图②, 点 $P, Q$ 分别到达点 $B, A$ 后继续运动, 点 $P$ 到达点 $C$ 后停止运动. 当 $t$ 为何值时, $A Q=\frac{1}{2} C P$ ?
【探究】若点 $P, Q$ 分别到达点 $B, A$ 后继续沿着 $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$ 的方向运动, 请直接写出点 $P$ 与点 $Q$ 第一次相遇时, 相遇点的位置.