单选题 （共 5 题 ），每题只有一个选项正确
如图，光滑水平地面上有一小车，一轻弹簧的一端与车厢的挡板相连，另一端与滑块相连，滑块与车厢的水平底板间有摩擦。用力向右推动车厢使弹簧压缩，撤去推力时滑块在车厢底板上有相对滑动。在地面参考系（可视为惯性系）中，从撤去推力开始，小车、弹簧和滑块组成的系统
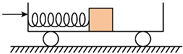
$\text{A.}$ 动量守恒，机械能守恒
$\text{B.}$ 动量守恒，机械能不守恒
$\text{C.}$ 动量不守恒，机械能守恒
$\text{D.}$ 动量不守恒，机械能不守恒
如图 (a), 在一块很大的接地金属平板的上方固定一负电荷。由于静电感应, 在金属平板 上表面产生感应电荷, 金属板上方电场的等势面如图 (b) 中虚线所示, 相邻等势面间的电势 差都相等。若将一正试探电荷先后放于 $M$ 和 $\mathrm{N}$ 处, 该试探电荷受到的电场力大小分别为 $F_M$ 和 $F_N$, 相应的电势能分别为 $E_{\mathrm{p} M}$ 和 $E_{\mathrm{p} N}$, 则
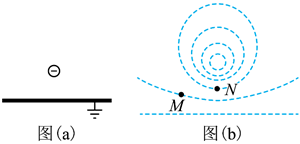
$\text{A.}$ $ F_M < F_N, E_{p M}>E_{p N} $
$\text{B.}$ $F_M>F_N, E_{p M}>E_{p N}$
$\text{C.}$ $F_M < F_N, E_{p M} < E_{p N}$
$\text{D.}$ $F_M>F_N, E_{p M} < E_{p N}$
如图, 圆形区域内有垂直纸面向里的匀强磁场, 质量为 $m$ 、电荷量为 $q(q>0)$ 的带电粒子从 圆周上的 $M$ 点沿直径 $M O N$ 方向射入磁场。若粒子射入磁场时的速度大小为 $v_1$, 离开磁场时 速度方向偏转 $90^{\circ}$; 若射入磁场时的速度大小为 $v_2$, 离开磁场时速度方向偏转 $60^{\circ}$, 不计重 力，则 $\frac{v_1}{v_2}$ 为
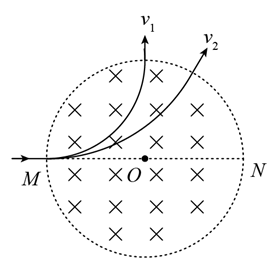
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{\sqrt{3}}{3}$
$\text{C.}$ $\frac{\sqrt{3}}{2}$
$\text{D.}$ $\sqrt{3}$
医学治疗中常用放射性核素 ${ }^{113} \mathrm{In}$ 产生 $\gamma$ 射线, 而 ${ }^{113} \mathrm{In}$ 是由半衰期相对较长的 ${ }^{113} \mathrm{Sn}$ 衰变产生的。对于质量为 $m_0$ 的 ${ }^{113} \mathrm{Sn}$, 经过时间 $t$ 后剩余的 ${ }^{113} \mathrm{Sn}$ 质量为 $m$, 其 $\frac{m}{m_0}-t$ 图线如图所示。从图中可以得到 ${ }^{113} \mathrm{Sn}$ 的半衰期为
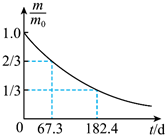
$\text{A.}$ $37.3d$
$\text{B.}$ $101.0d$
$\text{C.}$ $115.1d$
$\text{D.}$ $124.9d$
科学家对银河系中心附近的恒星S2进行了多年的持续观测，给出1994年到2002年间S2的位置如图所示。科学家认为S2的运动轨迹是半长轴约为 （太阳到地球的距离为 ）的椭圆，银河系中心可能存在超大质量黑洞。这项研究工作获得了2020年诺贝尔物理学奖。若认为S2所受的作用力主要为该大质量黑洞的引力，设太阳的质量为M，可以推测出该黑洞质量约为
$\text{A.}$ $4 \times 10^4 \mathrm{M}$
$\text{B.}$ $4 \times 10^6 \mathrm{M}$
$\text{C.}$ $4 \times 10^8 \mathrm{M}$
$\text{D.}$ $4 \times 10^{10} M$
多选题 （共 4 题 ），每题有多个选项正确
水平桌面上, 一质量为 $m$ 的物体在水平恒力 $F$ 拉动下从静止开始运动, 物体通过的路程等于 $s_0$ 时, 速度的大小为 $v_0$, 此时撤去 $F$, 物体继续滑行 $2 s_0$ 的路程后停止运动, 重力加速度大小为 $g$, 则
$\text{A.}$ 在此过程中 $F$ 所做的功为 $\frac{1}{2} m v_0^2$
$\text{B.}$ 在此过中 $F$ 的冲量大小等于 $\frac{3}{2} m v_0$
$\text{C.}$ 物体与桌面间的动摩擦因数等于 $\frac{v_0^2}{4 s_0 g}$
$\text{D.}$ $F$ 的大小等于物体所受滑动摩擦力大小的 2 倍
四个带电粒子的电荷量和质量分别 $(+q, m) 、(+q, 2 m) 、(+3 q, 3 m) 、(-q, m)$ 它们先后以 相同的速度从坐标原点沿 $x$ 轴正方向射入㕕匀强电场中, 电场方向与 $y$ 轴平行, 不计重力, 下 列描绘这四个粒子运动轨迹的图像中, 可能正确的是
$\text{A.}$ 
$\text{B.}$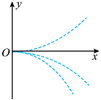 
$\text{C.}$ 
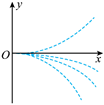$\text{D.}$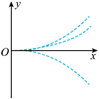 
水平地面上有一质量为 $m_1$ 的长木板, 木板的左明上有一质量为 $m_2$ 的物块, 如图 ( $a$ ) 所示。 用水平向右的拉力 $F$ 作用在物块上, $F$ 随时间 $t$ 的变化关系如图 (b) 所示, 其中 $F_1 、 F_2$ 分别 为 $t_1 、 t_2$ 时刻 $F$ 的大小。木板的加速度 $a_1$ 随时间 $t$ 的变化关系如图 (c) 所示。已知木板与地 面间的动摩擦因数为 $\mu_1$, 物块与木板间的动摩擦因数为 $\mu_2$, 假设最大静摩擦力均与相应的滑 动摩擦力相等, 重力加速度大小为 $g$ 。则
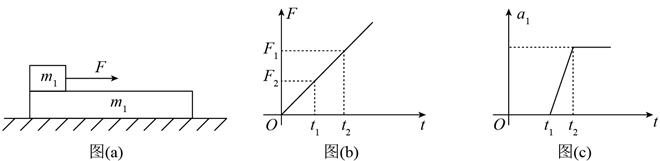
$\text{A.}$ $F_1=\mu_1 m_1 g$
$\text{B.}$ $F_2=\frac{m_2\left(m_1+m_2\right)}{m_1}\left(\mu_2-\mu_1\right) g$
$\text{C.}$ $\mu_2>\frac{m_1+m_2}{m_2} \mu_1$
$\text{D.}$ 在 $0 \sim t_2$ 时间段物块与木板加速度相等
如图, 一定量的理想气体从状态 $a\left(p_0, V_0, T_0\right)$ 经热力学过程 $a b 、 b c 、 c a$ 后又回到状 态 $a$ 。对于 $a b 、 b c 、 c a$ 三个过程, 下列说法正确的是
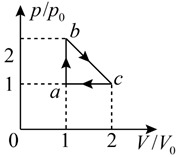
$\text{A.}$ $a b$ 过程中, 气体始终吸热
$\text{B.}$ $c a$ 过程中, 气体始终放热
$\text{C.}$ $c a$ 过程中, 气体对外界做功
$\text{D.}$ $b c$ 过程中, 气体的温度先降低后升高
$\text{E.}$ $b c$ 过程中, 气体的温度先升高后降低
填空题 （共 4 题 ），请把答案直接填写在答题纸上
某同学利用图（a）所示装置研究平抛运动的规律。实验时该同学使用频闪仪和照相机对做平抛运动的小球进行拍摄，频闪仪每隔 发出一次闪光，某次拍摄后得到的照片如图（b）所示（图中未包括小球刚离开轨道的影像）。图中的背景是放在竖直平面内的带有方格的纸板，纸板与小球轨迹所在平面平行，其上每个方格的边长为 。该同学在实验中测得的小球影像的高度差已经在图（b）中标出。
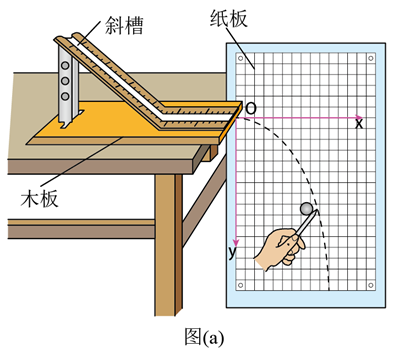
完成下列填空: (结果均保留 2 位有效数字)
(1) 小球运动到图 (b) 中位置 $A$ 时, 其速度的水平分量大小为 $\mathrm{m} / \mathrm{s}$, 竖直分量 大小为 $\mathrm{m} / \mathrm{s}$
(2) 根据图 (b) 中数据可得, 当地重力加速度的大小为 $\mathrm{m} / \mathrm{s}^2$
一实验小组利用图 (a) 所示的电路测量一电池的电动势 $E$ (约 $1.5 \mathrm{~V}$ ) 和内阻 $r$ (小于 $2 \Omega$ )。 图中电压表量程为 $1 \mathrm{~V}$, 内阻 $R_V=380.0 \Omega$ : 定值电阻 $R_0=20.0 \Omega$; 电阻箱 $R$, 最大阻值为 $999.9 \Omega ; \mathrm{S}$ 为开关。按电路图连接电路。完成下列填空:
(1) 为保护电压表, 闭合开关前, 电阻箱接入电路的电阻值可以选
$\Omega($ 填 “ 5.0 ”
或 “15.0”);
(2) 闭合开关, 多次调节电阻箱, 记录下阻值 $R$ 和电压表的相应读数 $U$;
(3) 根据图 (a) 所示电路, 用 $R 、 R_0 、 R_{\mathrm{V}} 、 E$ 和 $r$ 表示 $\frac{1}{U}$, 得 $\frac{1}{U}=$
(4) 利用测量数据, 做 $\frac{1}{U}-R$ 图线, 如图 (b) 所示:
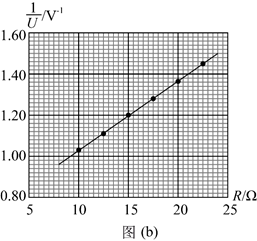
(5) 通过图（b）可得 $E=$ （ ） $\mathrm{V}$ (保留 2 位小数), $r=$ （ ） $\Omega$ (保留 1 位 小数);
(6) 若将图 (a) 中的电压表当成理想电表, 得到的电源电动势为 $E^{\prime}$, 由此产生的误差为 $\left|\frac{E^{\prime}-E}{E}\right| \times 100 \%=$ $\%$
一篮球质量为 $m=0.60 \mathrm{~kg}$, 幸运动员使其从距地面高度为 $h_1=1.8 \mathrm{~m}$ 处由静止自由落下, 反 弹高度为 $h_2=1.2 \mathrm{~m}$ 。若使篮球从距地面 $h_3=1.5 \mathrm{~m}$ 的高度由静止下落, 并在开始下落的同时 向下拍球、球落地后反弹的高度也为 $1.5 \mathrm{~m}$ 。假设运动员拍球时对球的作用力为恒力, 作用时 间为 $t=0.20 \mathrm{~s}$; 该篮球每次与地面碰撞前后的动能的比值不变。重力加速度大小取 $g=10 \mathrm{~m} / \mathrm{s}^2$, 不计空气阻力。求:
(1) 运动员拍球过程中对篮球所做的功;
(2) 运动员拍球时对篮球的作用力的大小。
如图, 一倾角为 $\alpha$ 的光滑固定斜面的顶端放有质量 $M=0.06 \mathrm{~kg}$ 的 U 型导体框, 导体框的电 阻忽略不计; 一电阻 $R=3 \Omega$ 的金属棒 $C D$ 的两端置于导体框上, 与导体框构成矩形回路 $C D E F ; E F$ 与斜面底边平行, 长度 $L=0.6 \mathrm{~m}$ 。初始时 $C D$ 与 $E F$ 相距 $s_0=0.4 \mathrm{~m}$, 金属棒 与导体框同时由静止开始下滑, 金属棒下滑距离 $s_1=\frac{3}{16} \mathrm{~m}$ 后进入二方向垂直于斜面的匀强磁 场区域, 磁场边界 (图中虚线) 与斜面底边平行; 金属棒在磁场中做匀速运动, 直至离开磁 场区域。当金属棒离开磁场的瞬间, 导体框的 $E F$ 边正好进入磁场, 并在匀速运动一段距离后 开始加速。已知金属棒与导体框之间始终接触良好, 磁场的磁感应强度大小 $B=1 \mathrm{~T}$, 重力加 速度大小取 $g=10 \mathrm{~m} / \mathrm{s}^2, \sin \alpha=0.6$ 。求:
(1) 金属棒在磁场中运动时所受安培力的大小;
（2）金属棒的质量以及金属棒与导体框之间的动摩擦因数;
（3）导体框匀速运动的距离。
解答题 （共 3 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
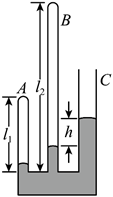
如图, 一玻璃装置放在水平桌面上, 坚直玻璃管 A、B、C 粗细均匀, A、B 两管的上端封闭, $\mathrm{C}$ 管上端开口, 三管的下端在同一水平面内且相互连通。 $\mathrm{A} 、 \mathrm{~B}$ 两管的长度分别为 $l_1=13.5 \mathrm{~cm}$, $l_2=32 \mathrm{~cm}$ 。将水银从 C 管缓慢注入, 直至 $\mathrm{B} 、 \mathrm{C}$ 两管内水银柱的高度差 $h=5 \mathrm{~cm}$ 。已知外界 大气压为 $p_0=75 \mathrm{cmHg}$ 。求 $\mathrm{A} 、 \mathrm{~B}$ 两管内水银柱的高度差。
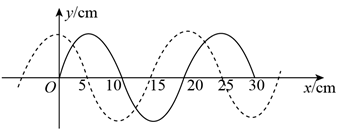
图中实线为一列简谐横波在某一时刻的波形曲线, 经过 $0.3 \mathrm{~s}$ 后, 其波形曲线如图中虚线所示。 已知该波的周期 $T$ 大于 $0.3 \mathrm{~s}$, 若波是沿 $x$ 轴正方向传播的, 则该波的速度大小为 （ ） $\mathrm{m} / \mathrm{s}$, 周期为 （ ） $\mathrm{s}$, 若波是沿 $x$ 轴负方向传播的, 该波的周期为 （ ） S。
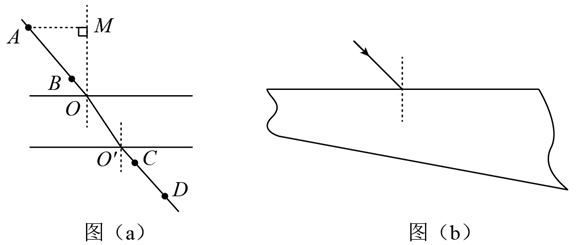
用插针法测量上、下表面平行的玻璃砖的折射率。实验中用 $\mathrm{A} 、 \mathrm{~B}$ 两个大头针确定入射光路、 C、D 两个大头针确定出射光路, $O$ 和 $O^{\prime}$ 分别是入射点和出射点, 如图 ( $a$ ) 所示。测得玻璃 砖厚度为 $h=15.0 \mathrm{~mm}, \mathrm{~A}$ 到过 $O$ 点的法线 $O M$ 的距离 $A M=10.0 \mathrm{~mm}, M$ 到玻璃砖的距离 $M O=20.0 \mathrm{~mm}, O^{\prime}$ 到 $O M$ 的距离为 $s=5.0 \mathrm{~mm}$ 。
(i) 求玻璃砖的折射率;
（ii）用另一块材料相同, 但上下两表面不平行的玻璃砖继续实验, 玻璃砖的截面如图 (b) 所示。光从上表面入射, 入时角从 0 逐渐增大, 达到 $45^{\circ}$ 时、玻璃砖下表面的出射光线恰好消 失。求此玻璃砖上下表面的夹角。
