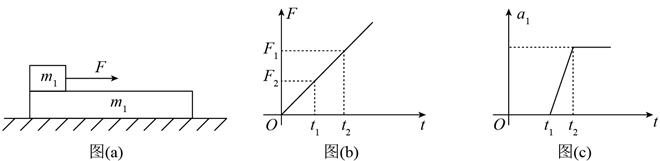
水平地面上有一质量为 $m_1$ 的长木板, 木板的左明上有一质量为 $m_2$ 的物块, 如图 ( $a$ ) 所示。 用水平向右的拉力 $F$ 作用在物块上, $F$ 随时间 $t$ 的变化关系如图 (b) 所示, 其中 $F_1 、 F_2$ 分别 为 $t_1 、 t_2$ 时刻 $F$ 的大小。木板的加速度 $a_1$ 随时间 $t$ 的变化关系如图 (c) 所示。已知木板与地 面间的动摩擦因数为 $\mu_1$, 物块与木板间的动摩擦因数为 $\mu_2$, 假设最大静摩擦力均与相应的滑 动摩擦力相等, 重力加速度大小为 $g$ 。则
A
$F_1=\mu_1 m_1 g$
B
$F_2=\frac{m_2\left(m_1+m_2\right)}{m_1}\left(\mu_2-\mu_1\right) g$
C
$\mu_2>\frac{m_1+m_2}{m_2} \mu_1$
D
在 $0 \sim t_2$ 时间段物块与木板加速度相等
E
F