单选题 (共 6 题 ),每题只有一个选项正确
设二维随机向量 $(X, Y)$ 的联合分布列为
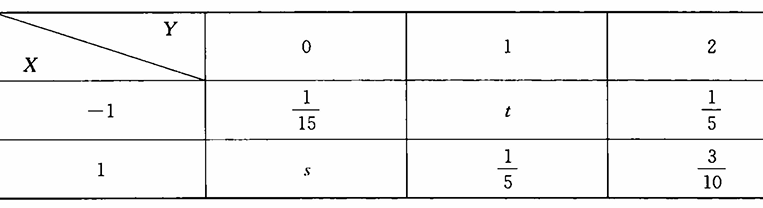
若要使 $X$ 与 $Y$ 相互独立,则 $(s, t)$ 取
$\text{A.}$ $\left(\frac{2}{10}, \frac{1}{15}\right)$ ;
$\text{B.}$ $\left(\frac{1}{15}, \frac{2}{10}\right)$ ;
$\text{C.}$ $\left(\frac{1}{10}, \frac{2}{15}\right)$ ;
$\text{D.}$ $\left(\frac{2}{15}, \frac{1}{10}\right)$ .
设随机变量 $X$ 的 $E(X)=\mu, D(X)=\sigma^2(\sigma>0)$ ,则对任意常数 $c$ ,必有( ).
$\text{A.}$ $E\left[(X-c)^2\right]=E\left(X^2\right)-c^2$ ;
$\text{B.}$ $E\left[(X-c)^2\right] \geqslant E\left[(X-\mu)^2\right]$ ;
$\text{C.}$ $E\left[(X-c)^2\right] < E\left[(X-\mu)^2\right]$ ;
$\text{D.}$ $E\left[(X-c)^2\right]=E\left[(X-\mu)^2\right]$ .
设 $\left(X_1, X_2, \cdots, X_8\right)$ 和 $\left(Y_1, Y_2, \cdots, Y_{10}\right)$ 为分别来自两个正态总体 $N\left(-1,2^2\right)$ 及 $N\left(2,5^2\right)$ 的样本,且相互独立.$S_1^2, S_2^2$ 分别为两个样本的方差,则服从 $F(7,9)$ 分布的统计量是 。
$\text{A.}$ $\frac{2 S_1^2}{5 S_2^2}$ ;
$\text{B.}$ $\frac{5 S_1^2}{2 S_2^2}$ ;
$\text{C.}$ $\frac{4 S_2^2}{25 S_1^2}$ ;
$\text{D.}$ $\frac{25 S_1^2}{4 S_2^2}$ .
设随机变量 $U \sim N(0,1)$ ,对给定的 $\alpha(0 < \alpha < 1)$ ,分位点 $u_\alpha$ 满足 $P(U> \left.u_a\right)=\alpha$ .若 $P(|U| < c)=\alpha$ ,则 $c=$ .
$\text{A.}$ $u_{\frac{\alpha}{2}}$ ;
$\text{B.}$ $u_{1-\frac{a}{2}}$ ;
$\text{C.}$ $u_{\frac{1-a}{2}}$ ;
$\text{D.}$ $u_{1-\alpha}$.
要使 $P(X=k)=a t^k, k=1,2, \cdots$ 为离散型随机变量 $X$ 的分布列,则
$\text{A.}$ $t=(1+a)^{-1}$ 且 $a>0$ ;
$\text{B.}$ $a=1-t$ 且 $0 < t < 1$ ;
$\text{C.}$ $a=t^{-1}-1$ 且 $t < 1$ ;
$\text{D.}$ $a>0$ 且 $0 < t < 1$ .
设随机变量 $X$ 和 $Y$ 独立同分布,记 $U=X+Y, V=X-Y$ ,则随机变量 $U$和 $V$ 必然 .
$\text{A.}$ 相互独立;
$\text{B.}$ 不相互独立;
$\text{C.}$ 相关;
$\text{D.}$ 不相关.
填空题 (共 6 题 ),请把答案直接填写在答题纸上
设 $A, B, C$ 为三个随机事件,表示事件 $D=\{A, B, C$ 中不多于一个发生 $\}=$
将红、黄、蓝 3 个球随机地放人 4 个盒子,若每个盒子容纳球数不限,则有 3个盒子各放一个球的概率 $p=$
已知二维随机变量 $(X, Y) \sim N(1,2 ; 2,4 ; 0)$ ,设随机变量 $Z=2 X+Y-$ 3 ,则 $Z$ 的密度函数 $f_Z(z)=$
设假设检验中犯第一类错误的概率为 $\alpha$ ,犯第二类错误的概率为 $\beta$ .为了同时减少 $\alpha$ 和 $\beta$ ,那么只有
设 $X$ 是区间 $[0,1]$ 上的连续型随机变量,已知 $P(X \leqslant 0.3)=0.8$ ,且 $Y= 1-X$ ,则当常数 $c=$ $\_\_\_\_$时,有 $P(Y \leqslant c)=0.2$
在处理快艇的 6 次试验数据中,得到最大航速 $v$ 的 6 个数据(单位: $\mathrm{m} / \mathrm{s}$ ):
$$
27,38,30,37,35,31
$$
则数学期望 $E(V)$ 的无偏估计值是 $\_\_\_\_$ ;方差 $D(V)$ 的无偏估计值是 $\_\_\_\_$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
飞机有三个不同部分遭到射击,在第 $i$ 部分被击中 $i$ 发子弹时,飞机才会被击落.射击的命中率与每一部分的面积成正比,三个部分的面积之比为 $1: 2: 7$ .若飞机已被击中 2 弹,求飞机被击落的概率.
设二维随机变量 $(X, Y)$ 在区域 $D=\{(x, y) \mid 0 < x < 2,0 < y < 1\}$ 上服从均匀分布,令
$$
U=\left\{\begin{array}{ll}
0, & X < Y, \\
1, & X \geqslant Y,
\end{array} \quad V= \begin{cases}0, & X < 2 Y, \\
1, & X \geqslant 2 Y,\end{cases}\right.
$$
求:(1)$(U, V)$ 的联合分布列;
(2)相关系数 $\rho_{U V}$ 。
光明电脑公司出售平板电脑,这种电脑的使用寿命 $X$ 服从参数为 0.25 的指数分布.按统一规定:出售该种电脑在一年内非人为损坏的可给予调换,但只能调换一次.该公司每售出一台电脑可盈利 200 元,调换一台则付出 300 元.问该年度内,公司销售该种电脑多少台,可使盈利的期望达到 10 万元?
设二维随机变量 $(X, Y)$ 的联合密度
$$
f(x, y)= \begin{cases}3 y, & 0 < x < y, 0 < y < 1, \\ 0, & \text { 其他. }\end{cases}
$$
求:随机变量 $Z=X-2 Y$ 的密度 $f_Z(z)$ .
设总体 $X$ 的密度为
$$
f(x ; \theta)=\left\{\begin{array}{ll}
\frac{1}{\theta} \mathrm{e}^{-\frac{x-\mu}{\theta}}, & x \geqslant \mu, \\
0, & x < \mu,
\end{array} \quad(\mu, \theta \text { 未知 }),\right.
$$
$\left(X_1, X_2, \cdots, X_n\right)$ 为来自总体的一个样本.求 $\mu, \theta$ 的最大似然估计量.
某种产品的一项质量指标 $X \sim N\left(\mu, \sigma^2\right)$ ,在 5 次独立的测试中,测得数据 (单位: cm ):
$$
1.23,1.22,1.20,1.26,1.23 .
$$
试检验:(1)可否认为该指标的数学期望 $\mu=1.23 \mathrm{~cm}$ ?
(2)若指标的标准差 $\sigma \leqslant 0.015$ ,是否可认为这次测试的标准差显著偏大?
$$
\left[\chi_{0.05}^2(4)=9.488, t_{0.025}(4)=2.7764\right](\alpha=0.05)
$$
证明题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设随机变量 $X$ 和 $Y$ 相互独立,且方差 $D(X), D(Y), D(X Y)$ 存在.证明:
$$
D(X Y) \geqslant D(X) D(Y) .
$$