单选题 (共 5 题 ),每题只有一个选项正确
事件 $\mathrm{A}, \mathrm{B}$ 相互独立,则
$\text{A.}$ $\mathrm{A}, \mathrm{B}$ 互斥
$\text{B.}$ $\mathrm{A}, \mathrm{B}$ 对立
$\text{C.}$ $\mathrm{P}(\mathrm{AB})=\mathrm{P}(\mathrm{A}) \mathrm{P}(\mathrm{B})$
$\text{D.}$ $P(A B)=0$
当( )成立时,一定有随机变量 $\mathrm{X}, \mathrm{Y}$ 相互独立。
$\text{A.}$ $f(x, y)=f_X(x) f_Y(y)$ ,
$\text{B.}$ $\rho_{X Y}=0$ ,
$\text{C.}$ $\mathrm{D}(\mathrm{X}+\mathrm{Y})=\mathrm{D}(\mathrm{X})+\mathrm{D}(\mathrm{Y})$
$\text{D.}$ $\mathrm{E}(\mathrm{XY})=\mathrm{E}(\mathrm{X}) \mathrm{E}(\mathrm{Y})$
总体是 $X,\left(X_1, X_2\right)$ 是简单随机样本,下列都是总体的数学期望的无偏估计量,其中最有效的是:( )
$\text{A.}$ $0.9 X_1+0.1 X_2$
$\text{B.}$ $0.8 X_1+0.2 X_2$
$\text{C.}$ $0.7 X_1+0.3 X_2$
$\text{D.}$ $0.6 X_1+0.4 X_2$
随机变量 X 的密度函数是 $f=\left\{\begin{array}{cc}\sqrt{a^2-x^2} & |x| < a \\ 0 & \text { 其他 }\end{array}, a= \right.$ 。
$\text{A.}$ $\frac{2}{\pi}$
$\text{B.}$ $\sqrt{\frac{2}{\pi}}$
$\text{C.}$ $\frac{\pi}{2}$
$\text{D.}$ $\sqrt{\frac{\pi}{2}}$
n 个小球随机放入 n 个充分大的盒子里,每个盒子里只有一个小球的概率是
$\text{A.}$ $\frac{n!}{n^n}$
$\text{B.}$ $\frac{n}{n^n}$
$\text{C.}$ $\frac{1}{n!}$
$\text{D.}$ $\frac{1}{n}$
填空题 (共 10 题 ),请把答案直接填写在答题纸上
$A, B, C$ 是三个随机事件,用 $A, B, C$ 表示其中至少一个发生
袋中装有 3 个黑球, 4 个红球,从中一次随机摸出 3 个球,至少有一个黑球的概率是
袋中装有 3 个黑球, 4 个红球,从中一次随机摸出 3 个球,已知取出的球有黑色,则取出的球中至少有一个红球的概率是
随机变量 $X_1 \sim N(2,9), X_2 \sim N(1,4)$ ,且相互独立,$\frac{1}{5}\left(X_1-2 X_2\right)$ 服从的分布是 (要指明参数)
随机变量 $X$ 分布律是:
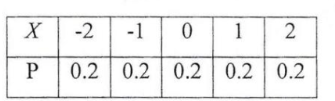
$\mathrm{D}(X)=$
$X_1, X_2, \cdots X_n \cdots$ 是独立同分布的随机变量序列,$X_i \sim E(\lambda)$ ,当 $n \rightarrow \infty$ , $\bar{X}=\frac{1}{n} \sum_{i=1}^n X_i$ 依概率收敛于
n 重伯努利试验中,事件 $A$ 每次发生的概率是 0.2 ,根据中心极限定理,当 n 充分大时,事件 $A$ 出现的频率近似分布是 (要指明参数)。
总体 $X \sim N\left(\mu, \sigma^2\right),\left(X_{:}, X_2, \cdots X_n\right)$ 是简单随机样本,则 $\frac{\bar{X}-\mu}{\frac{S}{\sqrt{n}}}$ 服从自由度为 $\_\_\_\_$ 的 t 分布
总体 $X \sim N\left(\mu, \sigma^2\right),\left(X_1, X_2, \cdots X_n\right)$ 是简单随机样本,$\sigma^2$ 是已知参数,则 $\mu$ 的置信度为 $1-\alpha$ 的双侧置信区间是
总体是 $X$ ,数学期望是 $\mu,\left(X_1, X_2, X_3\right)$ 是简单随机样本, $a\left(X_1+X_2\right)+b\left(X_2+X_3\right)$ 是 $\mu$ 的无偏估计量,则 $a+b=\frac{1}{2}$
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在数字通信中,由于存在随机干扰,因此接收到的信号有误差。发报机发出信号 0 的概率是 0.8 ,发出信号 1 的概率是 0.2 .当发出信号 0 的时候,收到信号 1 的概率是 0.3 .当发出信号 1 的时候,收到信号 1 的概率是 0.9 .试计算当接收到信号 1 的时候,发报机发出是信号 1 的概率。
随机变量 $X \sim N(0,1), Y=|X|$ ,求随机变量 $Y$ 的概率密度函数。
随机变量 $X$ 的密度函数是 $f(x)=\left\{\begin{array}{cc}a x^2 & x \in[-1,0] \\ b x & x \in(0,1] \\ 0 & \text { 其他 }\end{array}, \quad E(X)=\frac{1}{12}\right.$ 。试计算系数 $a, b$
已知随机变量 $X$ 在区间 $[0,1]$ 服从均匀分布,随机变量 $Y$ 在区间 $[0,1]$ 服从均匀分布,且 $X, Y$ 相互独立。求随机变量 $Z=X+Y$ 的概率密度函数。
甲乙两人独立地,等可能地,各自向区间 $[0,1]$ 内随机投掷一个点。求两人投掷的点之间的距离大于 $\frac{1}{2}$ 的概率
二维随机变量 $(X, Y)$ 在三角形 D 内服从均匀分布。 D 由直线, $\mathrm{x}=0, \mathrm{y}=0, \mathrm{x}+\mathrm{y}=1$ 围成。求 $\mathrm{E}(X Y)$
测量一个物理量的值总有误差的,因此测量值是随机变量,设它服从 $N(3,0.22^2)$ ,进行 n 次重复测量。要求 n 次测量的平均值在区间 $(2.9,3.1)$ 内的概率 $\geq 0.9$ .问至少要重复测量多少次?$z_{0.05}=1.65, z_{0.1}=1.29$
设总体 $X$ 的概率密度是 $f(x)=\left\{\begin{array}{cc}\lambda e^{-\lambda x} & x>0, \quad \lambda>0 \text { ,是未知参数,样本观测 } \\ 0 & x < 0\end{array}\right.$值 $\left(x_1, x_2, \cdots x_n\right)$ ,求 $\lambda$ 的极大似然估计量。
设某天的自动包装机包装的每包产品重量服从正态分布,从中随机抽取 25 包,算得平均重量是 46 克,标准差 10 克,问在显著性水平 0.05 下,可否认为这天的包装机包装产品每包平均重量是 50 克.并给出检验过程。$t_{0.05}(24)=1.7109, t_{0.025}(24)=2.0639$