单选题 (共 3 题 ),每题只有一个选项正确
在三棱锥 $P-A B C$ 中,$P A \perp$ 底面 $A B C, C A=C B=P A=2, \angle A C B=\frac{2 \pi}{3}$ ,则三棱锥 $P-A B C$ 外接球的表面积为
$\text{A.}$ $25 \pi$
$\text{B.}$ $20 \pi$
$\text{C.}$ $16 \pi$
$\text{D.}$ $12 \pi$
已知正四棱锥 $P-A B C D$ 的底面边长为 $2 \sqrt{2}$ ,侧棱 $P A$ 与底面 $A B C D$ 所成的角为 $45^{\circ}$ ,顶点 $P, A, B, C, D$在球 $O$ 的球面上,则球 $O$ 的体积是
$\text{A.}$ $16 \pi$
$\text{B.}$ $\frac{32}{3} \pi$
$\text{C.}$ $8 \pi$
$\text{D.}$ $\frac{8 \sqrt{2}}{3} \pi$
已知圆锥内切球(与圆锥侧面、底面均相切的球)的半径为 2 ,当该圆锥的表面积最小时,其外接球的表面积为( )
$\text{A.}$ $81 \pi$
$\text{B.}$ $96 \pi$
$\text{C.}$ $108 \pi$
$\text{D.}$ $126 \pi$
多选题 (共 3 题 ),每题有多个选项正确
在 $\triangle A B C$ 中,$A B \perp B C$ ,且 $A C=2, B C=1$ ,若将 $\triangle A B C$ 沿 $A C$ 边上的中线 $B D$ 折起,使得平面 $A B D \perp$ 平面 $B C D$ .点 $E$ 在由此得到的四面体 $A B C D$ 的棱 $A C$ 上运动,则下列结论正确的为
$\text{A.}$ $\angle A D C=\frac{\pi}{2}$
$\text{B.}$ 四面体 $A B C D$ 的体积为 $\frac{1}{8}$
$\text{C.}$ 存在点 $E$ 使得 $V B D E$ 的面积为 $\frac{1}{4}$
$\text{D.}$ 四面体 $A B C D$ 的外接球表面积为 $\frac{13 \pi}{3}$
在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑(biēnào).如图,三棱锥 $D-A B C$ 为一个鳖臑,其中 $D A \perp$ 平面 $A B C, A B \perp B C, D A=A B=B C=2, A M \perp D C, M$ 为垂足,则
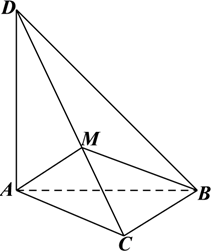
$\text{A.}$ $A M \perp$ 平面 $B C D$
$\text{B.}$ $D C$ 为三棱锥 $D-A B C$ 的外接球的直径
$\text{C.}$ 三棱锥 $M-A B D$ 的外接球体积为 $4 \sqrt{3} \pi$
$\text{D.}$ 三棱锥 $M-A B C$ 的外接球体积与三棱锥 $M-A B D$ 的外接球体积相等
已知四面体 $A B C D$ 的一个平面展开图如图所示,其中四边形 $A E F D$ 是边长为 $2 \sqrt{2}$ 的菱形,$B, C$ 分别为 $A E$ , $F D$ 的中点,$B D=2 \sqrt{2}$ ,则在该四面体中( )
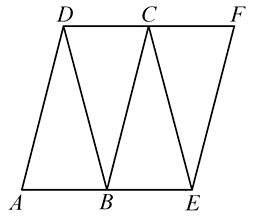
$\text{A.}$ $B E \perp C D$
$\text{B.}$ $B E$ 与平面 $D C E$ 所成角的余弦值为 $\frac{\sqrt{210}}{15}$
$\text{C.}$ 四面体 $A B C D$ 的内切球半径为 $\frac{\sqrt{105}}{30}$
$\text{D.}$ 四面体 $A B C D$ 的外接球表面积为 $9 \pi$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知四面体 $A-B C D$ 中,$A B=C D=\sqrt{5}, A C=B D=\sqrt{10}, B C=A D=\sqrt{13}$ ,则其外接球的体积为
如图,$D E$ 是边长为 4 的等边三角形 $A B C$ 的中位线,将 $V A D E$ 沿 $D E$ 折起,使得点 A 与 $P$ 重合,平面 $P D E \perp$平面 $B C D E$ ,则四棱锥 $P-B C D E$ 外接球的表面积是

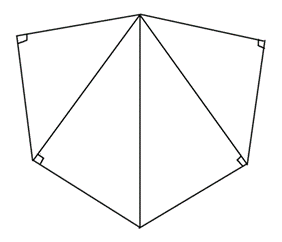
如图所示的由 4 个直角三角形组成的各边长均为 1 的六边形是某棱锥的侧面展开图,则该棱锥的内切球半径为 $\qquad$ .
已知三棱锥 $P-A B C$ 的所有棱长都相等,现沿 $P A, P B, P C$ 三条侧棱剪开,将其表面展开成一个平面图形,若这个平面图形外接圆的半径为 $2 \sqrt{6}$ ,则三棱锥 $P-A B C$ 的内切球的体积为