单选题 （共 17 题 ），每题只有一个选项正确
青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据 $L$ 和小数记录表的数据 $V$ 的满足 $L=5+\lg V$ ．已知某同学视力的五分记录法的数据为 4.9 ，则其视力的小数记录法的数据为 $(\quad)(\sqrt[10]{10} \approx 1.259)$
$\text{A.}$ 1.5
$\text{B.}$ 1.2
$\text{C.}$ 0.8
$\text{D.}$ 0.6
已知 $a=\log _5 2, b=\log _8 3, c=\frac{1}{2}$ ，则下列判断正确的是
$\text{A.}$ $c < b < a$
$\text{B.}$ $b < a < c$
$\text{C.}$ $a < c < b$
$\text{D.}$ $a < b < c$
已知 $9^m=10, a=10^m-11, b=8^m-9$ ，则
$\text{A.}$ $a>0>b$
$\text{B.}$ $a>b>0$
$\text{C.}$ $b>a>0$
$\text{D.}$ $b>0>a$
设 $a=2 \ln 1.01, b=\ln 1.02, c=\sqrt{1.04}-1$ ．则
$\text{A.}$ $a < b < c$
$\text{B.}$ $b < c < a$
$\text{C.}$ $b < a < c$
$\text{D.}$ $c < a < b$
已知 $5^5 < 8^4, 13^4 < 8^5$ ．设 $a=\log _5 3, b=\log _8 5, c=\log _{13} 8$ ，则（ ）
$\text{A.}$ $a < b < c$
$\text{B.}$ $b < a < c$
$\text{C.}$ $b < c < a$
$\text{D.}$ $c < a < b$
已知函数 $f(x)=\lg \left(x^2-4 x-5\right)$ 在 $(a,+\infty)$ 上单调递增，则 $a$ 的取值范围是（ ）
$\text{A.}$ $(2,+\infty)$
$\text{B.}$ $[2,+\infty)$
$\text{C.}$ $(5,+\infty)$
$\text{D.}$ $[5,+\infty)$
函数 $f ( x )=\log _2\left(- x ^2+2 \sqrt{2}\right)$ 的值域为 $(\quad)$
$\text{A.}$ $\left(-\infty, \frac{3}{2}\right)$
$\text{B.}$ $\left(-\infty, \frac{3}{2}\right]$
$\text{C.}$ $\left(\frac{3}{2},+\infty\right)$
$\text{D.}$ $\left[\frac{3}{2},+\infty\right)$
当 $a>1$ 时，在同一坐标系中，函数 $y=a^{-x}$ 与 $y=\log _a x$ 的图象为
$\text{A.}$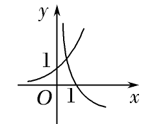 
$\text{B.}$ 
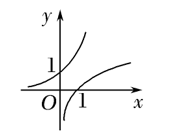$\text{C.}$ 
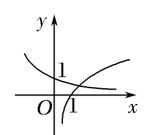$\text{D.}$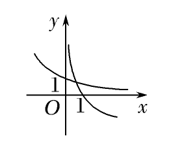 
已知 $a=\log _2 0.2, b=2^{0.2}, c=0.2^{0.3}$ ，则（ ）
$\text{A.}$ $a < b < c$
$\text{B.}$ $a < c < b$
$\text{C.}$ $c < a < b$
$\text{D.}$ $b < c < a$
区块链作为一种新型的技术，已经被应用于许多领域．在区块链技术中，某个密码的长度设定为 $512 B$ ，则密码一共有 $2^{512}$ 种可能，为了破解该密码，最坏的情况需要进行 $2^{512}$ 次运算．现在有一台计算机，每秒能进行 $1.25 \times 10^{13}$ 次运算，那么在最坏的情况下，这台计算机破译该密码所需时间大约为（ ）（参考数据： $\lg 2 \approx 0.3$ ， $\sqrt{10} \approx 3.16$ ）
$\text{A.}$ $6.32 \times 10^{141} s$
$\text{B.}$ $6.32 \times 10^{140} s$
$\text{C.}$ $3.16 \times 10^{141} s$
$\text{D.}$ $3.16 \times 10^{140} s$
已知函数 $f(x)=x \ln \left( e ^{2 x}+1\right)-x^2+1, f(a)=2$ ，则 $f(-a)$ 的值为 $(\quad)$
$\text{A.}$ 1
$\text{B.}$ 0
$\text{C.}$ -1
$\text{D.}$ -2
已知函数 $f(x)$ 是 $R$ 上的奇函数，当 $x>0$ 时，$f(x)=\ln x+\frac{a}{2 x}$ ，若 $f( e )+f(0)=-3$ ， e 是自然对数的底数，则 $f(-1)=(\quad)$
$\text{A.}$ e
$\text{B.}$ 2 e
$\text{C.}$ 3 e
$\text{D.}$ 4 e
设 $a=\log _5 4, b=\log _4 3, c=\left(\frac{1}{4}\right)^{0.6}$ ，则 $(\quad)$
$\text{A.}$ $a>b>c$
$\text{B.}$ $c>b>a$
$\text{C.}$ $b>a>c$
$\text{D.}$ $a>c>b$
已知 $a=7^{-\frac{1}{3}}, b=\log _7 2-2 \log _7 3, c=\left(\frac{1}{7}\right)^{\frac{1}{2}}$ ，则下列关系正确的是
$\text{A.}$ $a < b < c$
$\text{B.}$ $b < a < c$
$\text{C.}$ $c < b < a$
$\text{D.}$ $b < c < a$
已知函数 $f(x)=\log _a\left(2^x+b-1\right)(a>0$ ，且 $a \neq 1)$ 的图象如图所示，则 $a, b$ 满足的关系是
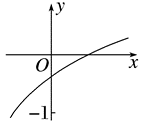
$\text{A.}$ $0 < a^{-1} < b < 1$
$\text{B.}$ $0 < b < a^{-1} < 1$
$\text{C.}$ $0 < b^{-1} < a < 1$
$\text{D.}$ $0 < a^{-1} < b^{-1} < 1$
已知 $a, b, c$ 为正实数，满足 $\left(\frac{1}{2}\right)^a=\log _2 a,\left(\frac{1}{2}\right)^b=b^2, c^{\frac{1}{2}}=2^{-c}$ ，则 $a, b, c$ 的大小关系为
$\text{A.}$ $a < c < b$
$\text{B.}$ $b < c < a$
$\text{C.}$ $c < a < b$
$\text{D.}$ $c < b < a$
在如今这个 5 G 时代， 6 G 研究已方兴未艾． 2021 年 8 月 30 日第九届未来信息通信技术国际研讨会在北京举办．会上传出消息，未来 6 G 速率有望达到 1 Tbps ，并启用毫米波，太赫兹，可见光等尖端科技，有望打造出空天地融合的立体网络，预计 6 G 数据传输速率有望比 5 G快 100 倍，时延达到亚毫秒级水平。香农公式 $C=W \log _2\left(1+\frac{S}{N}\right)$ 是被广泛公认的通信理论基础和研究依据，它表示：在受噪声干扰的信道中，最大信息传递率 $C$ 取决于信道带宽 $W$ ，信道内信号的平均功率 $S$ ，信道内部的高斯噪声功率 $N$ 的大小，其中 $\frac{S}{N}$ 叫做信噪比．若不改变带宽 $W$ ，而将信噪比 $\frac{S}{N}$ 从 11 提升至 499 ，则最大信息传递率 $C$ 会提升到原来的（ ）参考数据： $\log _2 3=1.58, \log _2 5=2.32$ ．
$\text{A.}$ 2.4 倍
$\text{B.}$ 2.5 倍
$\text{C.}$ 2.6 倍
$\text{D.}$ 2.7 倍
多选题 （共 2 题 ），每题有多个选项正确
已知函数 $f(x)$ 的图象与 $g(x)=2^x$ 的图象关于直线 $y=x$ 对称，令 $h(x)=f(1-|x|)$ ，则关于函数 $h(x)$ 有下列说法，其中正确的说法为
$\text{A.}$ $h(x)$ 的图象关于原点对称
$\text{B.}$ $h(x)$ 的图象关于 $y$ 轴对称
$\text{C.}$ $h(x)$ 的最大值为 0
$\text{D.}$ $h(x)$ 在区间 $(-1,1)$ 上单调递增
已知 $0 < b < a < 1$ ，则下列不等式成立的是
$\text{A.}$ $\log _a b < \log _b a$
$\text{B.}$ $\log _a b>1$
$\text{C.}$ $a \ln b < b \ln a$
$\text{D.}$ $a \ln a>b \ln b$
填空题 （共 5 题 ），请把答案直接填写在答题纸上
函数 $y=\log _a(x-2)+2(a>0$ 且 $a \neq 1)$ 的图象恒过定点
函数 $f(x)=\log _2(2 x+1)$ 的单调增区间为
若方程 $4^x=\log _\alpha x$ 在 $\left(0, \frac{1}{2}\right.$ ］上有解，则实数 $a$ 的取值范围为
已知函数 $f(x)=\log _a(8-a x)(a>0$ ，且 $a \neq 1)$ ，若 $f(x)>1$ 在区间［1，2］上恒成立，则实数 $a$ 的取值范围是
已知函数 $f(x)=\left|\log _2 x\right|$ ，实数 $a, b$ 满足 $0 < a < b$ ，且 $f(a)=f(b)$ ．若 $f(x)$ 在 $\left[a^2, b\right]$ 上的最大值为2,则 $\frac{1}{a}+b=$
解答题 （共 2 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=\left(2 \log _4 x-2\right)\left(\log _4 x+\frac{1}{2}\right)$ ．
（1）当 $x \in[1,16]$ 时，求该函数的值域；
（2）求不等式 $f(x)>2$ 的解集；
已知函数 $f(x)=\lg \frac{k x-1}{x-1}(k \in R )$ ．
（1）当 $k=0$ 时，求函数 $f(x)$ 的值域；
（2）当 $k>0$ 时，求函数 $f(x)$ 的定义域；
（3）若函数 $f(x)$ 在区间 $[10,+\infty)$ 上是单调增函数，求实数 $k$ 的取值范围．