单选题 (共 8 题 ),每题只有一个选项正确
已知全集 $U=\{1.2,3,4.5 .6\}, A=\{1.2 .3\}, B=\{2,3.4 .5\}$, 则图中阴影部分对应的集合为
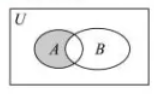
$\text{A.}$ $\{1\}$
$\text{B.}$ $\{2,3\}$
$\text{C.}$ $\{4,5\}$
$\text{D.}$ $\{6\}$
已知 $\bar{e}_1, \bar{e}_2$ 是不共线的单位向量, 若 $\vec{a}=\bar{e}_1+2 \bar{e}_2, \vec{b}=\lambda \overline{e_1}-\overline{e_2}$, 且 $\bar{a} // \vec{b}$, 则 $\lambda=(\quad)$
$\text{A.}$ 2
$\text{B.}$ -2
$\text{C.}$ $-\frac{1}{2}$
$\text{D.}$ $\frac{1}{2}$
下列四个函数中, 以 $\left(\frac{\pi}{2}, 0\right)$ 为其对称中心, 且在区间 $\left(0, \frac{\pi}{2}\right)$ 上单调递增的是()
$\text{A.}$ $y=\cos x$
$\text{B.}$ $y=\tan x$
$\text{C.}$ $y=\sin x$
$\text{D.}$ $y=|\cos x|$
已知函数 $f(x)=\left\{\begin{array}{l}-x-1, x \leq 0 \\ \ln (x+1), x>0\end{array}\right.$, 则关于 $x$ 的不等式 $f(x) < 1$ 的解集为
$\text{A.}$ $(-\infty,-2] \cup[e,+\infty)$
$\text{B.}$ $[-2, e]$
$\text{C.}$ $(-\infty,-2] \cup[e-1,+\infty)$
$\text{D.}$ $[-2, e-1]$
"直线 $a x+b y-1=0$ 与圆 $x^2+y^2=2$ 有公共点"是" $a^2+b^2 \geq 1$ "的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
某袋子中有大小相同的 4 个白球和 2 个红球, 甲乙两人先后依次从袋中不放回职球, 每次取 1 球, 先取到红球者获胜,则甲获胜的概率()
$\text{A.}$ $\frac{8}{15}$
$\text{B.}$ $\frac{4}{5}$
$\text{C.}$ $\frac{3}{5}$
$\text{D.}$ $\frac{2}{3}$
已知双曲线: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$, 过 $M(-2 a, 0)$ 的直线分别交双曲线左右两支为 $A, B, A$ 关于原点 $O$ 的对称点为 $C$, 若 $2 \angle B M O+\angle M B C=\frac{\pi}{2}$, 则双曲线的高心率 $e=()$
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ $2 \sqrt{2}$
$\text{D.}$ $2 \sqrt{3}$
已知 $f(x)$ 是定义在 R 上且不恒为 0 的连续函数, 若 $f(x+y)+f(x-y)=f(x) f(y), f(1)=0$, 则
$\text{A.}$ $f(0)=-2$
$\text{B.}$ $f(x)$ 为奇函数
$\text{C.}$ $f(x)$ 的周期为 2
$\text{D.}$ $-2 \leq f(x) \leq 2$
多选题 (共 3 题 ),每题有多个选项正确
下列说法正确的是()
$\text{A.}$ 若随机变量 $\xi \sim B\left(8, \frac{1}{4}\right)$, 则 $D(\xi)=\frac{3}{2}$
$\text{B.}$ 殖差平方和越大, 模型的拟合效果越好
$\text{C.}$ 若随机变量 $\eta \sim N\left(\mu, \sigma^2\right)$, 则当 $\mu$ 减小时, $P(|\eta-\mu| < \sigma)$ 保持不变
$\text{D.}$ 一组数据的极差不小于该组数据的标准差
某校南门前有条长 80 米, 宽 8 米的公路(如图矩形 $A B C D$ ), 公路的一侧划有 16 个长 5 米宽 2.5 米的停车位(如矩形 $A E F G$ ),由于停车位不足,放学时段造成道路拥堵,学校提出一个改造方案,在不改变停车位的大小和汽车通道宽度的条件下,通过压缩道路边绿化带及改变停车位方向来增加停车位,记绿化带被压缩的宽度 $A M=3$ (米), 停车位相对道路倾斜的角度 $\angle E^{\prime} A^{\prime} M=\alpha$, 其中 $\alpha \in\left(\frac{\pi}{6}, \frac{\pi}{3}\right)$, 则
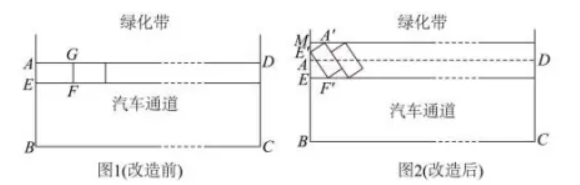
$\text{A.}$ $\cos \alpha=\frac{4}{5}$
$\text{B.}$ $\cos \alpha=\frac{3}{5}$
$\text{C.}$ 该路段改造后的停车位比改造前增加 8 个
$\text{D.}$ 该路段改造后的停车位比改造前增加 9 个
如图, $A B C D$ 是边长为 2 的正方形, $A A_1, B B_1, C C_1, D D_1$ 都垂直于底面 $A B C D$, 且 $D D_1=\frac{3}{2} A A_1=\frac{3}{2} C C_1=3 B B_1=3$, 点 $E$ 在线段 $C C_1$ 上, 平面 $B E D_1$ 交线段 $A A_1$ 于点 $F$, 则
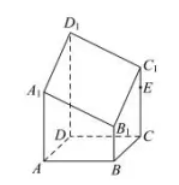
$\text{A.}$ $A_1, B_1, C_1, D_1$ 四点不共面
$\text{B.}$ 该几何体的体积为 8
$\text{C.}$ 过四点 $A_1, C_1, B, D$ 四点的外接球表面积为 $12 \pi$
$\text{D.}$ 截面四边形 $B E D_1 F$ 的周长的最小值为 10
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知 i 为虚数单位, 若 $z \cdot \bar{z}+z-\bar{z}=9+4 i$, 则 $|z|=$
已知等比数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 若 $S_{2 n}=\left(3^n+1\right) S_n$, 则 $\frac{S_6}{S_2}=$
已知函数 $f(x)= e ^x- e ^{-x}-\frac{1}{2} \sin 2 x+1$, 若对任意 $x \in(1,+\infty), f(a \ln x)+f(-x) < 2$, 则实数 $a$ 的取值范围为
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
每个正整数 $k$ 有唯一的"阶乘表示"为 $\left(a_1, a_2, \ldots, a_m\right)$, 这些 $a_i$ 满足 $k=1!\cdot a_1+2!\cdot a_2+\cdots+m!\cdot a_m$,其中每个 $a_t\left(i=1,2,3 \cdots, m, m \in N^*\right)$ 都是整数,且 $0 \leq a_i \leq i, a_m>0$ 。
(1) 求正整数 $3,4,5,6$ 的"阶乘表示";
(2) 若正整数 $k$ 对应的"阶乘表示"为 $\left(a_1, a_2, \ldots, a_m\right)$ ,正整数 $k^{\prime}$ 对应的"阶乘表示" $\left(a_1^{\prime}, a_2^{\prime}, \ldots, a_x^{\prime}\right)$ $\left(a_1, a_2, \cdots, a_s\right)$, 其中 $m>s$, 求证: $k>k^{\prime}$ ;
(3) 对正整数 $k$, 记 $b_n=\left[\frac{k}{n!}\right]\left(n \leq m, n \in N^*\right),[x]$ 表示不超过 $x$ 的最大整数, 数列 $\left\{(n-1) b_n\right\}$ 前 $n$ 项和为 $S_n$, 若 $k-S_m=2024$, 当 $k$ 最小时, 求 $a_m$ 的值.